 We find the critical values by solving the boundary equation:
We find the critical values by solving the boundary equation:
 Which breaks into these two equations:
Which breaks into these two equations:
 or
or 
 or
or 
 or
or 
 or
or  We also have a third critical value x=0 because
that is what we get when we set the denominator
in the original problem = 0.
So we put those points on a number line
----------------o----o--o------------------
-2 -1 -1/2 0 1/4 1 2
We test a value left of -1/2, say -1, in the
original inequality:
We also have a third critical value x=0 because
that is what we get when we set the denominator
in the original problem = 0.
So we put those points on a number line
----------------o----o--o------------------
-2 -1 -1/2 0 1/4 1 2
We test a value left of -1/2, say -1, in the
original inequality:



 That's true, so we shade the region left of -1/2
<================o----o--o------------------
-2 -1 -1/2 0 1/4 1 2
We test a value between -1/2 and 0, say -.2 in the
original inequality:
That's true, so we shade the region left of -1/2
<================o----o--o------------------
-2 -1 -1/2 0 1/4 1 2
We test a value between -1/2 and 0, say -.2 in the
original inequality:




 That's false, so we DO NOT shade the region between
-1/2 and 0
We test a value between 0 and 1/4, say .2 in the
original inequality:
That's false, so we DO NOT shade the region between
-1/2 and 0
We test a value between 0 and 1/4, say .2 in the
original inequality:




 That's false, so we DO NOT shade the region between
0 and 1/4.
We test a value right of 1/4, say 1, in the
original inequality:
That's false, so we DO NOT shade the region between
0 and 1/4.
We test a value right of 1/4, say 1, in the
original inequality:








 That's true so we shade -1/2
<================@----o--o=================>
-2 -1 -1/2 0 1/4 1 2
Now we test the endpoint 1/4
That's true so we shade -1/2
<================@----o--o=================>
-2 -1 -1/2 0 1/4 1 2
Now we test the endpoint 1/4




 That's true so we shade 1/4
<================@----o--@=================>
-2 -1 -1/2 0 1/4 1 2
So the solution set is:
That's true so we shade 1/4
<================@----o--@=================>
-2 -1 -1/2 0 1/4 1 2
So the solution set is:




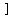

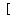



 Edwin
Edwin