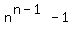SOLUTION: show that the number {{{n^(n-1)-1}}} is divisible by 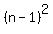{{{(n-1)^2}}} whenever {{{n>=2}}}

Lemma: there exists non-negative integer q such that



Proof:

By a factorization theorem 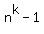 can be factored as:



where there are k terms in the second parentheses



Therefore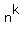 

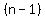
or there exists positive integer q such that



Thus the lemma is proved.



where there are n-1 terms in the parentheses on the right.

Now we wish to show that

 is a positive integer.  Factoring the numerator:









By the lemma, there exist 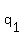,,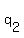... 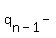so
that the preceding expression equals





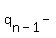
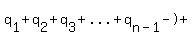
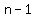since there are  terms this becomes:



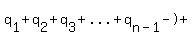
or

,

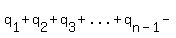
which is a positive integer.

Edwin