Question 288717: I have to use the critical value method solve the rational inequality.
Problem: 
I have no clue what the formula is to solve this. Any help is appreciated, thank you!! In the mean time, I'll keep sorting through the lessons on this site to see if I can find the one that pertains to this type.
Answer by texttutoring(324)   (Show Source): (Show Source):
You can put this solution on YOUR website! This would be easier to answer with a number line picture, but I don't know how to insert pictures here, so I'll try my best. If you want to see a picture, just message me.
First, state the unrestricted value(s). x cannot equal 1 (because the bottom cannot be zero).
Next, factor the top of the equation to find the critical values:
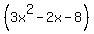
Ask yourself, what multiplies to -8? Your options are 4 and 2, or 8 and 1. Try this one:

Use FOIL to check that it's correct, and we find that it is. Therefore the critical values are:
3x+4=0 -> x=-4/3
and
x-2=0 -> x=2
On a number line, plot these two critical values, as well as the asymptote at 1. Use test points to find out in which intervals the inequality is true. You have four intervals to test:
I : x < -4/3
II: -4/3 < x < 1
III: 1 < x < 2
IV: x > 2
After trying some test values, you should find that only intervals II and IV are true. Your answer is:
-4/3 < x < 1
or
x > 2
Hopefully that helps. Let me know if you need clarifications.
|
|
|