Question 288548: The value of a particular investment follows a pattern of exponential growth. In the year 2000, you invested money in a money market account. The value of your investment t years after 2000 is given by the exponential growth model A=3000e^0.053t. When will the account be worth $5097?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! Invest money into money market account in year 2000.
Investment is for T years.
The formula for investment growth with continuous compounding is:
 . .
F = Future Amount.
P = Present Amount.
I = Annual Interest Rate
T = Number of Years
They have given you the formula as:
 . .
This is the same formula, except that they have replaced F with A and they have replaced P with 3000 and they have replaced I with .053.
Apparently, the money invested in the year 2000 is $3000 and the Annual Interest Rate is .053.
e is the scientific constant of 2.718281828...
The question they are asking is when you will have $5097 in the account.
$5097 is the future amount.
replace A with $5097 and your equation becomes:

Divide both sides of this equation by 3000 to get:

Take the log of both sides of this equation to get:
 . .
Since, in general, 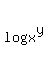 = = 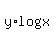 , your equation becomes: , your equation becomes:
 . .
Divide both sides of this equation by  to get: to get:
 . .
Use the log function of your calculator to find the log of (5097/3000) to get  . .
Use the log function of your calculator to find the log of  to get to get 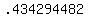 . .
Substitute these values into your equation of  to get: to get:
 . .
Solve for T to get:
T = 10.00075175.
That's the number of years it will take for $3000 invested in the year 2000 to reach $5079 given that the annual interest rate is .053 and continuous compounding is used.
To confirm, plug that value into your original equation to see if it is true.
Your original equation is:
 . .
Replace T with 10.00075175 to get:
 . .
Simplify to get:
 . .
Simplify further to get:
 . .
Simplify further to get:
 . .
The equation is true, so your answer is good.
That answer is:
The account will be worth $5097 in the year 2000 + 10.00075175 which would be the year 2010.
You start off with $3000 in the year 2000.
Sometime in the tenth year after, your account will be worth $5097.
A year by year analysis of your investment growth would look like the following:
year money
2000 $3000
2001 $3163
2002 $3335
2003 $3517
2004 $3708
2005 $3912
2006 $4123
2007 $4347
2008 $4584
2009 $4833
2010 $5096.796926
The figure in the year 2010 is equivalent to $3000*e^(.053*10).
The actual answer is $3000*e^(.053*10.00075175). This gives you exactly $5097.
It's a little more than 10 years, but that falls in the year 2010 anyway, so the answer, given in what year it occurs, is 2010.
10.00075175 years is equivalent to:
10 years and .274570421 days if we assume 1 year = 365.242199 days days in a year.
That puts you into January 1st of the year 2010.
|
|
|