SOLUTION: use Descartes's Rule of Signs to determine the possible number of positive and negative real zeros for the given function. f(x)=x^5-1.7x^4-17.65x^3+3x^2+45x-15.411

Algebra ->  Rational-functions -> SOLUTION: use Descartes's Rule of Signs to determine the possible number of positive and negative real zeros for the given function. f(x)=x^5-1.7x^4-17.65x^3+3x^2+45x-15.411      Log On


   

Question 288534: use Descartes's Rule of Signs to determine the possible number of positive and negative real zeros for the given function.
f(x)=x^5-1.7x^4-17.65x^3+3x^2+45x-15.411
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!

f%28x%29=x%5E5-1.7x%5E4-17.65x%5E3%2B3x%5E2%2B45x-15.411

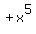The 1st term is %22%22%2Bx%5E5, That has a positive sign.

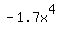The 2nd term is -1.7x%5E4.  That has a negative sign.  Therefore
going from the positive 1st term to the negative 2nd term is a sign 
change.  So far there is 1 sign change.

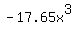The 3rd term is -17.65x%5E3.  That has a negative sign.  Therefore
going from the negative 2nd term to the negative 3rd term is NOT a sign 
change.  So far there is still just 1 sign change.

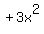The 4th term is %22%22%2B3x%5E2.  That has a positive sign.  Therefore
going from the negative 3rd term to the positive 4th term is a sign 
change.  So far there are now 2 sign changes.

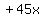The 5th term is %22%22%2B45x.  That has a positive sign.  Therefore
going from the positive 4th term to the positive 5th term is NOT a sign 
change.  So far there are still just 2 sign changes.

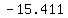The 6th term is -15.411.  That has a negative sign.  Therefore
going from the positive 5th term to the negative 6th term is a sign 
change.  So far there are now 3 sign changes.

We have reached the end of the polynomial.  It has 3 sign changes.

So there could be 3 positive zeros.  There could also be 1 positive
zero, because the number of positive zeros could either be the number
of sign changes, or a multiple of 2 fewer positive zeros. 

So there are either 3 or 1 positive zero.

Next substitute -x for x and simplify:

f%28-x%29=%28-x%29%5E5-1.7%28-x%29%5E4-17.65%28-x%29%5E3%2B3x%5E2%2B45x-15.411

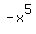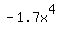f%28-x%29=-x%5E5-1.7x%5E4%2B17.65x%5E3%2B3x%5E2-45x-15.411

The 1st term is -x%5E5, That has a negative sign.

The 2nd term is -1.7x%5E4.  That has a negative sign.  Therefore
going from the negative 1st term to the negative 2nd term is NOT a sign 
change.  So far there are no sign changes.

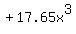The 3rd term is %22%22%2B17.65x%5E3.  That has a positive sign.  Therefore
going from the negative 2nd term to the positive 3rd term is a sign 
change.  So far there is now just 1 sign change.

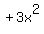The 4th term is %22%22%2B3x%5E2.  That has a positive sign.  Therefore
going from the positive 3rd term to the positive 4th term is NOT a sign 
change.  So far there is still just 1 sign change.

The 5th term is -45x.  That has a negative sign.  Therefore
going from the positive 4th term to the negative 5th term is a sign 
change.  So far there are now 2 sign changes.

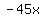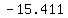The 6th term is -15.411.  That has a negative sign.  Therefore
going from the negative 5th term to the negative 6th term is NOT a sign 
change.  So far there are still 2 sign changes.

So there could be 2 negative zeros.  There could also be 0 negative
zeros, because the number of negative zeros could either be the number
of sign changes, or a multiple of 2 fewer negative zeros. 

So there are either 2 or 0 negative zeros.

Edwin