SOLUTION: For the given circle, find the x-intercepts and the y-intercepts. x^2+y^2-10x+4y+13=0 This is what I have so far: To find the x-intercepts let y=0 X^2-10x+13=0 (x+___)

Algebra ->  Coordinate-system -> SOLUTION: For the given circle, find the x-intercepts and the y-intercepts. x^2+y^2-10x+4y+13=0 This is what I have so far: To find the x-intercepts let y=0 X^2-10x+13=0 (x+___)      Log On


   

Question 288447: For the given circle, find the x-intercepts and the y-intercepts.
x^2+y^2-10x+4y+13=0
This is what I have so far:
To find the x-intercepts let y=0
X^2-10x+13=0
(x+___)(x-___) but this equation doesn't factor into integers as 13 is a prime number

Found 2 solutions by richwmiller, Alan3354:
Answer by richwmiller(17219) About Me  (Show Source):
You can put this solution on YOUR website!
This circle crosses the x axis twice but never crosses the y axis at all.
You have to complete the square twice to find the center and radius. The y intercepts are not integers either.
The center is at integer points and the radius is an integer.
But the problem doesn't ask for those.

Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
For the given circle, find the x-intercepts and the y-intercepts.
x^2+y^2-10x+4y+13=0
This is what I have so far:
To find the x-intercepts let y=0
X^2-10x+13=0
this equation doesn't factor into integers as 13 is a prime number
Most of life is not integers.
--------------
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B-10x%2B13+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-10%29%5E2-4%2A1%2A13=48.

Discriminant d=48 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--10%2B-sqrt%28+48+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-10%29%2Bsqrt%28+48+%29%29%2F2%5C1+=+8.46410161513775
x%5B2%5D+=+%28-%28-10%29-sqrt%28+48+%29%29%2F2%5C1+=+1.53589838486225

Quadratic expression 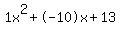1x%5E2%2B-10x%2B13 can be factored:
1x%5E2%2B-10x%2B13+=+%28x-8.46410161513775%29%2A%28x-1.53589838486225%29
Again, the answer is: 8.46410161513775, 1.53589838486225. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-10%2Ax%2B13+%29


-----------------------
The x-intercepts are not integers.
------------
To get the y-intercepts:
y^2 + 4y + 13 = 0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B4x%2B13+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%284%29%5E2-4%2A1%2A13=-36.

The discriminant -36 is less than zero. That means that there are no solutions among real numbers.

If you are a student of advanced school algebra and are aware about imaginary numbers, read on.


In the field of imaginary numbers, the square root of -36 is + or - sqrt%28+36%29+=+6.

The solution is x%5B12%5D+=+%28-4%2B-i%2Asqrt%28+-36+%29%29%2F2%5C1+=++%28-4%2B-i%2A6%29%2F2%5C1+, or
Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B4%2Ax%2B13+%29

----------------
There are no real numbers solutions --> no y-intercepts.
--------------
If you complete the square:
x^2+y^2-10x+4y= -13
x^2-10x+25 + y^2+4y+4 = 16
x-5%29%5E2+%2B+%28y%2B2%29%5E2+=+4%5E2
The center of the circle is (5,-2) and its radius is 4.
It's 5 units to the right with a radius of 4, --> no y-intercepts.