Question 288406: whats 3 consecutive integers such that the sum of the squares of the smaller two is equal to the square of the largest
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Recall that consecutive integers follow the pattern: x, x+1, x+2, ...
So the statement "3 consecutive integers such that the sum of the squares of the smaller two is equal to the square of the largest" means that 
 Start with the given equation. Start with the given equation.
 FOIL FOIL
 Combine like terms. Combine like terms.
 Get every term to the left side. Get every term to the left side.
 Combine like terms. Combine like terms.
Notice that the quadratic  is in the form of is in the form of  where where  , ,  , and , and 
Let's use the quadratic formula to solve for "x":
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Negate Negate  to get to get  . .
 Square Square  to get to get  . .
 Multiply Multiply  to get to get 
 Rewrite Rewrite  as as 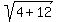
 Add Add  to to  to get to get 
 Multiply Multiply  and and  to get to get  . .
 Take the square root of Take the square root of  to get to get  . .
 or or  Break up the expression. Break up the expression.
 or or  Combine like terms. Combine like terms.
 or or  Simplify. Simplify.
So the solutions are  or or 
This means that the numbers are either: 3, 4, 5
OR
the numbers are: -1, 0, 1
|
|
|