|
Question 286756: Hello,
I can't seem to make sense of the simple definition of a rational number. I'm looking at my instructor's notes, and I've Googled it as well, but the definition seems contradictory to me. The definition I'm looking at says:
"numbers that "come to an end" or numbers that repeat and have a pattern. Examples of rational numbers are:
5.34, 0.131313..., 6/7, 2/3, 9"
I don't understand how it can be both. Which is it? Is it numbers that come to an end or is it numbers that DON'T come to an end? My understanding if IRrational numbers is that they do NOT come to an end, such as 33333....., so what is the difference?
Can anyone think of a different way to explain this? I'm sure it must be quite simple but it's just not clicking for me.
Thank you!
T
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website! Rational Number: Any number that can be represented as a fraction of two integers (whole numbers) where the denominator is not zero.
Examples:  ,  ,  ,  ,  ,  ,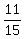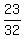 
Notes:
1) Every whole number or integer is a rational number since each whole number or integer can be represented as a fraction of that number over 1. Eg. the whole number 5 is a rational number since
2) We can divide out the fractions to get decimal values. For instance,  (where the 3's go on forever). Consequently, the number 0.333333 (where the 3's go on forever) is a rational number also. Notice how this number has a predictable pattern (we know that there will be a 3 a million digits down the line). The decimal representation may go on forever, but because it has a predictable pattern, this means that this number is rational. On the other hand,  (where the decimal digits go on....) has an unpredictable pattern of digits. In fact, it has no pattern at all. So the key here is a predictable pattern.
|
|
|
| |
