SOLUTION: (3^2x+1)^2=4.3^x+2 (Three to the two x plus one power squared is equal to 4.3 to the x+2 power) Thanks

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: (3^2x+1)^2=4.3^x+2 (Three to the two x plus one power squared is equal to 4.3 to the x+2 power) Thanks      Log On


   

Question 286299: (3^2x+1)^2=4.3^x+2
(Three to the two x plus one power squared is equal to 4.3 to the x+2 power)

Thanks
Found 2 solutions by richwmiller, jsmallt9:
Answer by richwmiller(17219) About Me  (Show Source):
You can put this solution on YOUR website!
This problem was submitted three times in 3 minutes
BTW is (2x+1) an exponent?

Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
It's a good thing you expressed the equation in English. For future reference, the way to express what you said in English is:
(3^(2x+1))^2=4.3^(x+2)
Without the additional parentheses, the +1 and +2 would not be part of the exponents. What you wrote would be:
%283%5E2x%2B1%29%5E2=4.3%5Ex%2B2
And the problem is simpler if it is 4*3 and not 4.3. In case it is 4*3, I will do that solution, too, at the end.)

%283%5E%282x%2B1%29%29%5E2=4.3%5E%28x%2B2%29
Now to solve the equation. First we will use the rule of exponents for raising a power to a power, i.e multiply the exponents:
3%5E%284x%2B2%29=4.3%5E%28x%2B2%29
Next we find the logarithm of each side. If you want the simplest exact expression for the solution, then you should use base 3 or base 4.3 logarithms. But if you want a decimal approximation of the solution then you should choose a base your calculator "knows", like base 10 or base e (ln). Since the exact solution is not going to be that simple I am going to use base 10:
log%28%283%5E%284x%2B2%29%29%29=log%28%284.3%5E%28x%2B2%29%29%29
Next we use a property of logarithms, log%28a%2C+%28p%5Eq%29%29+=+q%2Alog%28a%2C+%28p%29%29, to move the exponents of the arguments out in front. (This property of logarithms is the very reason we use logarithms on equations like this. It let's us move the variable, which is in the exponents, where we can "get at it" to solve for it.)
%284x%2B2%29log%28%283%29%29=%28x%2B2%29log%28%284.3%29%29
Using the Distributive Property to multiply these:
4x%2Alog%28%283%29%29%2B2log%28%283%29%29=x%2Alog%28%284.3%29%29%2B2log%28%284.3%29%29
Next we gather the terms with x on one side and the other terms on the other side of the equation:
4x%2Alog%28%283%29%29+-+x%2Alog%28%284.3%29%29=2log%28%284.3%29%29-2log%28%283%29%29
Then we'll factor out x on the left side:
x%284log%28%283%29%29+-+log%28%284.3%29%29%29=2log%28%284.3%29%29-2log%28%283%29%29
and divide both sides by 4log((3)) - log((4.3)):
x=%282log%28%284.3%29%29-2log%28%283%29%29%29%2F%284log%28%283%29%29+-+log%28%284.3%29%29%29
This is an exact expression for the solution. For a decimal approximation, get out your calculator to find a decimal approximation for the two logarithms (which each occur twice) and then simplify the right side.

In case the problem was 4*3 and not 4.3:
%283%5E%282x%2B1%29%29%5E2=4%2A3%5E%28x%2B2%29
3%5E%284x%2B2%29=4%2A3%5E%28x%2B2%29
Divide both sides by 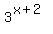3%5E%28x%2B2%29:
3%5E%284x%2B2%29%2F3%5E%28x%2B2%29=4
Using the rule of exponents for division we subtract the exponents:
3%5E%28%284x%2B2%29-%28x%2B2%29%29=4
3%5E%283x%29=4
Now we use logarithms. This time I'll use base 3:
log%283%2C+%283%5E%283x%29%29%29=log%283%2C+%284%29%29
3x%2Alog%283%2C+3%29%29=log%283%2C+%284%29%29
By definition log%283%2C+%283%29%29+=+1:
3x%2A1=log%283%2C+%284%29%29
3x=log%283%2C+%284%29%29
Divide both sides by 3:
x=log%283%2C+%284%29%29%2F3
This is an exact expression for the solution (to the problem with 4*3 and not 4.3). For a decimal approximation we will need to use the base conversion formula, log%28a%2C+%28p%29%29+=+log%28b%2C+%28p%29%29%2Flog%28b%2C+%28a%29%29, to convert the base 3 logarithm into an expression of base 10 logarithms:
x=log%28%284%29%29%2Flog%28%283%29%29%2F3
or:
x=log%28%284%29%29%2F3log%28%283%29%29
Use your calculator on the right side to get a decimal.