Question 286109: The owner of a tea shop wants to mix three kinds of tea to make 100oz of a mixture that will sell for $0.83 per oz. He uses Orange Pekoe, which sells for $0.80 per oz, Irish Breakfast, for $0.85 per oz, and Earl Grey which sells for $0.95 per oz. If he wants to use twice as much Orang Pekoe as Irish Breakfast, how much of each kind of tea should be used?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! The owner of a tea shop wants to mix three kinds of tea to make 100oz of a
mixture that will sell for $0.83 per oz.
He uses Orange Pekoe, which sells for $0.80 per oz, Irish Breakfast, for $0.85
per oz, and Earl Grey which sells for $0.95 per oz.
If he wants to use twice as much Orange Pekoe as Irish Breakfast, how much of
each kind of tea should be used?
:
Let x = amt of Irish breakfast tea required
It says,"use twice as much Orange Pekoe as Irish Breakfast", therefore:
2x = amt of Orange Pekoe Tea
:
Let y = amt of Earl Grey
:
Amt of tea equation
x + 2x + y = 100 oz
3x + y = 100
y = (100-3x)
:
Cost of tea equation
.85x + .80(2x) + .95y = .83(100)
.85x + 1.60x + .95y = 83
2.45x + .95y = 83
:
Replace y with (100-3x)
2.45x + .95(100-3x) = 83
2.45x + 95 - 2.85x = 83
2.45x - 2.85x = 83 - 95
-.40x = -12
x = 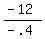
x = 30 oz of Irish Tea required
then
2(30) = 60 oz of Orange Pekoe
and
y = 100 - 90
y = 10 oz of Earl Grey
:
:
Check solution in cost equation
.85(30) + .80(60) + .95(10) = .83(100)
25.5 + 48.0 + 9.5 = 83
|
|
|