Question 285614: A rectangle is 4 times as long as it is wide. A second rectangle is 5 centimeters longer and 2 centimeters wider than the first. The area of the second rectangle is 270 square centimeters greater than the first. What are the dimensions of the original rectangle?
I would like to see how to solve the problem in steps, if possible. Thank you!
Found 2 solutions by JBarnum, MathTherapy:
Answer by JBarnum(2146)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let the width of the 1st rectangle be W. Then its length = 4W, since its length is 4 times its width
The width and length of the 2nd rectangle are W + 2, and 4W + 5, respectively, since the second rectangle is 2 centimeters wider and 5 centimeters longer than the 1st.
The area of the 1st rectangle is then: W*4W, or 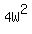 , and the area of the 2nd rectangle is (W + 2)(4W + 5 ), or , and the area of the 2nd rectangle is (W + 2)(4W + 5 ), or 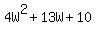 . .
Since the area of the 2nd rectangle is 270 square centimeters greater than the area of the 1st rectangle, then we’ll have:


- 13W = - 260

Now, since W, or width = 20, then the dimensions of the 1st rectangle are: W, or width =  cm, and L, or length = cm, and L, or length =  cm ------> 4W, or 4(20) cm ------> 4W, or 4(20)
Check:
Width of 1st rectangle = 20 cm
Length of 1st rectangle = 4(20) = 80 cm
Area of 1st rectangle = 20 * 80 = 1,600 sq centimeters
Width of 2nd rectangle = 22 cm (20 + 2)
Length of 2nd rectangle = 85 cm (4*20 + 5)
Area of 2nd rectangle = 22 * 85 = 1,870 sq centimeters
Area of 2nd rectangle (1,870 sq centimeters) is 270 sq centimeters greater than area of 1st rectangle (1,600 sq centimeters).
Send comments and “thank yous” to MathMadEzy@aol.com
|
|
|