|
Question 284738: i must figure the x intercepts, y intercepts and the foci of this ellipse? x^2/25 + y^2/36=1 please help me if at all possible.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! The general form of the equation for an ellipse is:
(x-h)^2 / a^2 + (y-k)^2 / b^2 = 1 if the major axis is horizontal.
The general form of the equation for an ellipse is:
(x-h)^2 / b^2 + (y-k)^2 / a^2 = 1 if the major axis is vertical.
a is the distance from the center of the ellipse to the intersection of the ellipse with the major axis of the ellipse.
b is the distance from the center of the ellipse to the intersection of the ellipse with the minor axis of the ellipse.
h is the x-coordinate of the vertex / center of the ellipse.
k is the y-coordinate of the vertex / center of the ellipse.
Your equation is:
x^2/25 + y^2/36 = 1
Since 36 is bigger than 25, Your a^2 term is under the y^2 term, and your b^2 term is under the x^2 term.
This means that your major axis is vertical.
Your equation fits the form of:
(x-h)^2 / b^2 + (y-k)^2 / a^2 = 1 where the major axis is vertical.
In your equation, h and k are equal to 0.
This means that the center / vertex of your ellipse is at the point (x,y) = (0,0)
The standard form of your equation becomes:
x^2 / b^2 + y^2 / a^2 = 1 where the major axis is vertical.
In your equation:
a = sqrt(a^2) = sqrt(36) = 6
b = sqrt(b^2) = sqrt(25) = 5
c is the distance from the center of the ellipse to the focal points of the ellipse.
The focal points of the ellipse lay on the major axis of the ellipse.
The formula to derive c is:
c^2 = a^2 - b^2
In your equation, this becomes:
c^2 = 36 - 25 = 11
This makes c = sqrt(11) which is equal to 3.31662479.
Rounded to the nearest 10th, c is equal to 3.3.
Your equation is, once again:
x^2/25 + y^2/36 = 1
To graph this equation, we solve for y.
Subtract x^2/25 from both sides of this equation to get:
y^2/36 = -x^2/25 + 1
Multiply both sides of this equation by 36 to get:
y^2 = -(36/25)*x^2 + 36
Take the square root of both sides of this equation to get:
y = +/- sqrt(-(36/25)*x^2 + 36)
Graph of this equation looks like this:
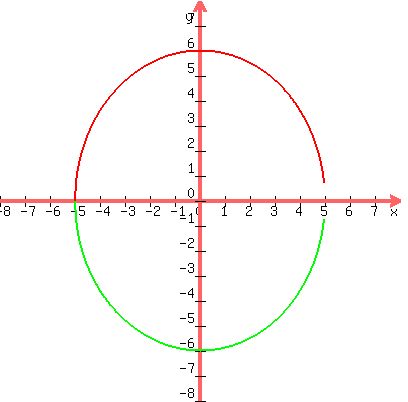
You can see that the length of the major axis is 12 which is equal to 2*a. The major axis of this ellipse is vertical.
You can also see that the length of the minor axis is 10 which is equal to 2*b. The minor axis of this ellipse is horizontal.
This is because a is equal to 6, and b is equal to 5.
The x-intercepts of this ellipse are the values of x when y = 0.
The equation is:
x^2/25 + y^2/36 = 1
Make y equal to 0 and your equation becomes:
x^2/25 = 1
Multiply both sides of this equation by 25 and it becomes:
x^2 = 25
Take square root of this equation to get:
x = +/- 5
You can see from the graph that when y = 0, x = +/- 5.
Likewise, your equation is, once again:
x^2/25 + y^2/36 = 1
Make x equal to 0 and the equation becomes:
y^2/36 = 1
Multiply both sides of this equation by 36 to get:
y^2 = 36
Take the square root of both sides of this equation to get:
y = +/- 6.
You can see from the graph that y = +/- 6 when x = 0.
You can't see the focal points from the graph, but we already solved for the focal points using the equation of c^2 = a^2 - b^2.
This got us c^2 = 36 - 25 = 11
This made c = +/- sqrt (11) which is roughly equivalent to +/- 3.3
That would be +/- the distance from the center of the ellipse, which is at (0,0).
this makes the focal points at (x,y) = (0,3.3), and (x,y) = 0,-3.3).
They are on the major axis of the ellipse which is vertical.
|
|
|
| |