SOLUTION: solve for x: 27^(x-2)=92^(x-1)

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: solve for x: 27^(x-2)=92^(x-1)      Log On


   

Question 283820: solve for x:
27^(x-2)=92^(x-1)
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
27%5E%28x-2%29+=+92%5E%28x-1%29
With the variable in one (or more) exponents, logarithms are often used to solve the equation. The base of the logarithm used does not make any significant difference. But if you are looking for the simplest, exact expression for the solution, then choose a base for the logarithm that matches the base of one of the exponents. If you are only interested in a decimal approximation of the solution, then choose a base for the logarithm that your calculator "knows" (like base 10 or base e (ln)).

First I am going find an exact solution. Then I will show you how to find a decimal approximation. To find the simplest, exact solution we should choose base 27 or base 92 logarithms. (For no reason in particular) I will use base 27:
log%2827%2C+%2827%5E%28x-2%29%29%29+=+log%2827%2C+%2892%5E%28x-1%29%29%29
Now we can use the property of logarithms, log%28a%2C+%28p%5Eq%29%29+=+q%2Alog%28a%2C+%28p%29%29, to move the exponents of the arguments out in front as coefficients. It is this very property that is the reason for using logarithms in the first place. It allows us to move the exponent(s), which has/have the variable in it, out in front where we "can get at it". Using the property on our equation we get:
%28x-2%29log%2827%2C+%2827%29%29+=+%28x-1%29log%2827%2C+%2892%29%29
Since log%2827%2C+%2827%29%29+=+1 by definition (this is why base 27 was a good choice), the left side simplifies to:
x-2+=+%28x-1%29log%2827%2C+%2892%29%29
Now that the x's are out where we can get at them, we can start solving for x. First simplify the right side:
x-2+=+x%2Alog%2827%2C+%2892%29%29+-+log%2827%2C+%2892%29%29
Next we gather the x terms on one side and the other terms on the other side (by subtracting x from and adding 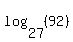log%2827%2C+%2892%29%29 to each side):
log%2827%2C+%2892%29%29-2+=+x%2Alog%2827%2C+%2892%29%29+-+x
Next we factor out x on the right side:
log%2827%2C+%2892%29%29-2+=+x%2A%28log%2827%2C+%2892%29%29+-+1%29
and then divide both sides by 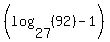%28log%2827%2C+%2892%29%29+-+1%29:
%28log%2827%2C+%2892%29%29-2%29%2F%28log%2827%2C+%2892%29%29+-+1%29+=+x
This is an exact expression for the solution.

If you want a decimal approximation for the solution you can a) use base 10 or base e logarithms instead of base 27; or b) use the base conversion formula on the above exact solution.

I will use the base conversion formula, log%28a%2C+%28p%29%29+=+log%28b%2C+%28p%29%29%2Flog%28b%2C+%28a%29%29, to convert the base 27 logarithms into base 10 logarithms:

Now that we have an expression on which we can use our calculators. If your calculator can handle parentheses, you can type this is pretty much as you see it. (I'd suggest putting parentheses around the "big" numerator and denominator.). If not, then
  1. Find the base 10 logarithm of 92.
  2. Find the base 10 logarithm of 27
  3. Divide the result from step 1 by the result from step 2.
  4. Subtract 2 from the result of step 3.
  5. Subtract 1 from the result of step 3.
  6. Divide the result of step 4 by the result of step 5.