Question 283657: If a gambler rolls two dice and gets a sum of 7, he wins $10, and if he gets a sum of 4, he wins $20. The cost to play the game is $5. What is the expectation (to the nearest cent) of this game?
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! If a gambler rolls two dice and gets a sum of 7, he wins $10, and if he gets a sum of 4, he wins $20. The cost to play the game is $5. What is the expectation (to the nearest cent) of this game?
There are three possible outcomes of playing the game:
A. He can pay $5 to play, roll a sum of 7, win $10, and net $5.
B. He can pay $5 to play, roll a sum of 4, win $20, and net $15.
C. He can pay $5 to play, roll a sum of neither 4 nor 7, and net -$5 (a loss).
Now we need to calculate the probabilities of doing those.
Here is the sample space of rolling a pair of dice:
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
There are 36 posasible rolls. The 6 red ones have sum 7, the 3 blue ones
have sum 4, the 27 black ones have some other sum. So
The probability of rolling a 7 is  or or  . P(A) = . P(A) =  The probability of rolling a 4 is
The probability of rolling a 4 is 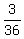 or or  . P(B) = . P(B) =  The probability of rolling neither of those sum is
The probability of rolling neither of those sum is  or or  P(C) =
P(C) =  To find the expectation, multiply each win by the probability of winning it,
then add them.
To find the expectation, multiply each win by the probability of winning it,
then add them.



  That means if one plays the game many times he will have
averaged losing
That means if one plays the game many times he will have
averaged losing 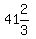 cents per game.
Edwin cents per game.
Edwin
|
|
|