Question 283392: I am having trouble figuring this problem out.
What is the probability of getting a license plate that has a repeated letter or digit if the sequence is 6 letters followed by 2 numerals, followed by 1 letter (rounded to the nearest 10th. The answer I am coming up with is 76.9%, which is apparently not right. This is how I was figuring it up.
(25/26)(24/25)(23/24)(22/23)(21/22)(20/21)+(9/10)(8/9)+(19/20)
Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website! I am having trouble figuring this problem out.
What is the probability of getting a license plate that has a repeated letter or digit if the sequence is 6 letters followed by 2 numerals, followed by 1 letter (rounded to the nearest 10th. The answer I am coming up with is 76.9%, which is apparently not right. This is how I was figuring it up.
(25/26)(24/25)(23/24)(22/23)(21/22)(20/21)+(9/10)(8/9)+(19/20).
No, I'm afraid that's not correct. It should be:
 .
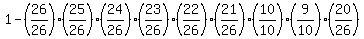We have to find the probability of the complement event and then subtract
from 1.
The complement event is that of having NO repeated letters or digits.
A sample license plate with no repeats is, say
M Q J W U P 7 4 D
The number of possible 7-letter sequences with no repeats is "26 position 7",
or "26P7". [It doesn't matter that the final D has two digits between it and
the P]. And for every one of those sequences there are "10 position 2"
sequences of 2 digits. That's 26P7*10P2.
Or. let's go through it step by step:
M Q J W U P 7 4 D
There are 26 ways to choose a letter to go where the M is. Having chosen the
letter to go where the M is,
there are 25 ways to choose a letter to go where the Q is. Having chosen the
letters to go where the M and Q are,
there are 24 ways to choose a letter to go where the J is. Having chosen the
letters to go where the M, Q, and J are,
there are 23 ways to choose a letter to go where the W is. Having chosen the
letters to go where the M, Q, J, and A are,
there are 22 ways to choose a letter to go where the U is. Having chosen the
letters to go where the M, Q, J, A, and U are,
there are 21 ways to choose a letter to go where the P is. Having chosen the
letters to go where the M, Q, J, A, U, and P are,
there are 10 ways to choose a digit to go where the 7 is. Having chosen the
letters to go where the M, Q, J, A, U, P are, and a digit to go where the
digit 7 is,
there are 9 ways to choose a digit to go where the 4 is. Having chosen the
letters to go where the M, Q, J, A, U, P are, and where the digits 7 and 4 are,
there are 20 ways to choose the letter on the right end where the D is.
So there are 26*25*24*23*22*21*10*9*20 ways to choose a license plate
with NO repeats.
The number of possible license plates with or without repeats is
26*26*26*26*26*26*10*10*26 =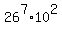 
The probability of the complement event is  .
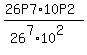Therefore the desired probability is
 , which rounds to 0.6.
Edwin
|
|
|
