x^2+4x+4-4y^2+8y-8=0
Is this an equation for a hyperbola?
Yes this is a hyperbola because the terms in  and
and  have opposite signs.
How do I find the center, vertices and foci?
First get it in standard form, which is either
have opposite signs.
How do I find the center, vertices and foci?
First get it in standard form, which is either
 if the hyperbola opens right and left,
or
if the hyperbola opens right and left,
or
 if the hyperbola opens upward and downward.
if the hyperbola opens upward and downward.
 The first three terms will factor into a perfect square as they
are. So we do so:
The first three terms will factor into a perfect square as they
are. So we do so:
 Add 8 to both side to get the loose number off the left side:
Add 8 to both side to get the loose number off the left side:
 Factor out the coefficient of
Factor out the coefficient of  out of the
last two terms on the left.
out of the
last two terms on the left.
 Complete the square on
Complete the square on 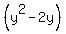 by multiplying
the coefficient of y, which is -2 by
by multiplying
the coefficient of y, which is -2 by  getting -1,
and then squaring -1, getting +1. And we add that inside the
second parentheses. However since there is a -4 in fromt of the
second parentheses, adding -1 inside the parentheses amounts
to adding
getting -1,
and then squaring -1, getting +1. And we add that inside the
second parentheses. However since there is a -4 in fromt of the
second parentheses, adding -1 inside the parentheses amounts
to adding 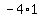 or -4 to the left side, so we must add -4
to the right side:
or -4 to the left side, so we must add -4
to the right side:
 Factor the trinomial as the square of a binomial, and combine
the numbers on the right:
Factor the trinomial as the square of a binomial, and combine
the numbers on the right:
 Get a 1 on the right by dividing through by 4
Get a 1 on the right by dividing through by 4

 Since the variable x comes first in the standard form, the
hyperbola opens right and left.
So we compare that to:
Since the variable x comes first in the standard form, the
hyperbola opens right and left.
So we compare that to:
 The center is (-2,1).
So we plot the center:
The center is (-2,1).
So we plot the center:

 so
so  , the semi-transverse axis is 2 unit
long, so we draw the complete transverse axis right and left
2 units from the center, that is, the tranverse axis is the
horizontal green line below:
, the semi-transverse axis is 2 unit
long, so we draw the complete transverse axis right and left
2 units from the center, that is, the tranverse axis is the
horizontal green line below:
 The vertices are the endpoints of the transverse axis,
so
the vertices are (-4,1) and (0,1)
The vertices are the endpoints of the transverse axis,
so
the vertices are (-4,1) and (0,1)
 so
so  , the semi-conjugate axis is 1 unit
long, so we draw the complete conjugate axis up and down
1 units from the center, that is, the conjugate axis is the
vertical green line below:
, the semi-conjugate axis is 1 unit
long, so we draw the complete conjugate axis up and down
1 units from the center, that is, the conjugate axis is the
vertical green line below:
 Now we draw in the defining rectangle
Now we draw in the defining rectangle
 Now we can draw the asymptotes which are the extended diagonals
of the defining rectangle:
Now we can draw the asymptotes which are the extended diagonals
of the defining rectangle:
 and we can sketch in the hyperbola:
and we can sketch in the hyperbola:
 Finally we will find the two foci. To do that,
we find c, which is the distance from the center to each
of the foci. We use the hyperbola Pythagorean relation:
Finally we will find the two foci. To do that,
we find c, which is the distance from the center to each
of the foci. We use the hyperbola Pythagorean relation:



 So the two foci are
So the two foci are 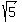 units right and
left of the center, and their coordinates are
(
units right and
left of the center, and their coordinates are
(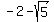 ,1) and (
,1) and (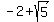 ,1)
or approximately the points:
(-4.2,1) and (.2,1)
,1)
or approximately the points:
(-4.2,1) and (.2,1)
 The hyperbola alone is just this, if you erase all the guidelines:
The hyperbola alone is just this, if you erase all the guidelines:
 Edwin
Edwin