
Subtract 1 from both sides to get 0 on the right
 Write
Write  as
as 
 Multiply top and bottom of
Multiply top and bottom of  by LCD
by LCD 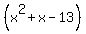

 Combine the two numerators over the common denominator:
Combine the two numerators over the common denominator:
 Remove the parentheses:
Remove the parentheses:
 Combine like terms on top:
Combine like terms on top:
 Find all critical values by setting numerator and
denominator = 0.
Setting numerator = 0
Find all critical values by setting numerator and
denominator = 0.
Setting numerator = 0
 discriminant =
discriminant =  discriminant =
discriminant =  discriminant is negative, so we don't
get any critical values from the numerator.
Setting denominator = 0
discriminant is negative, so we don't
get any critical values from the numerator.
Setting denominator = 0
 discriminant =
discriminant =  discriminant =
discriminant =  So we do get critical values from the
denominator:
So we do get critical values from the
denominator:



 So the two critical values are
So the two critical values are
 and
and  These are approximately 3.14 and -4.14
Put these on a number line:
------o----------------------o-----
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5
Choose a whole number value left of -4.14.
for a test value. The easiest is -5
Substitute in
These are approximately 3.14 and -4.14
Put these on a number line:
------o----------------------o-----
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5
Choose a whole number value left of -4.14.
for a test value. The easiest is -5
Substitute in
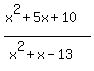

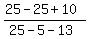
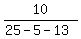
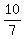 That is a positive number, so we put + signs over
that part of the number line:
+ + +
------o----------------------o-----
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5
Next choose a whole number value between the
two critical points for a test value. The
easiest is 0
Substitute in
That is a positive number, so we put + signs over
that part of the number line:
+ + +
------o----------------------o-----
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5
Next choose a whole number value between the
two critical points for a test value. The
easiest is 0
Substitute in
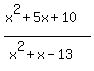
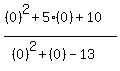
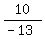
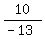
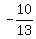 That is negative so we put - signs over that part
of the number line:
+ + + - - - - - - - - - -
------o----------------------o-----
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5
Choose a whole number value right of 3.14.
for a test value. The easiest is 4
Substitute in
That is negative so we put - signs over that part
of the number line:
+ + + - - - - - - - - - -
------o----------------------o-----
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5
Choose a whole number value right of 3.14.
for a test value. The easiest is 4
Substitute in
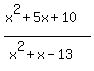

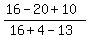
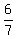 That is a positive number, so we put + signs over
that part of the number line:
+ + + - - - - - - - - - - + + +
------o----------------------o------
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5
Since the inequality of
That is a positive number, so we put + signs over
that part of the number line:
+ + + - - - - - - - - - - + + +
------o----------------------o------
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5
Since the inequality of
 is
is  we choose the intervals with + signs.
We cannot include the end points themselves
because they cause the denominator to be 0.
So the solution set is
(
we choose the intervals with + signs.
We cannot include the end points themselves
because they cause the denominator to be 0.
So the solution set is
( ,
, ) U (
) U (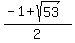 ,
,  )
Edwin
)
Edwin