Question 282922: rewrite without
the parentheses (2x+3)4
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
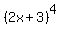 Start with the given expression Start with the given expression
To expand this, we're going to use binomial expansion. So let's look at Pascal's triangle:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
Looking at the row that starts with 1,4, etc, we can see that this row has the numbers:
1, 4, 6, 4, and 1
These numbers will be the coefficients of our expansion. So to expand 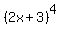 , simply follow this procedure: , simply follow this procedure:
Write the first coefficient. Multiply that coefficient with the first binomial term  and then the second binomial term and then the second binomial term  . Repeat this until all of the coefficients have been written. . Repeat this until all of the coefficients have been written.
Once that has been done, add up the terms like this:
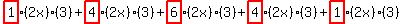 Notice how the coefficients are in front of each term. Notice how the coefficients are in front of each term.
However, we're not done yet.
 Looking at the first term Looking at the first term 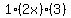 , raise , raise  to the 4th power and raise to the 4th power and raise  to the 0th power. to the 0th power.
 Looking at the second term Looking at the second term 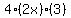 raise raise  to the 3rd power and raise to the 3rd power and raise  to the 1st power. to the 1st power.
Continue this until you reach the final term.
Notice how the exponents of  are stepping down and the exponents of are stepping down and the exponents of  are stepping up. are stepping up.
So the fully expanded expression should now look like this:
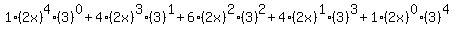
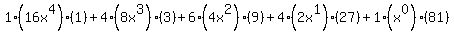 Distribute the exponents Distribute the exponents
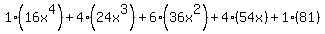 Multiply Multiply
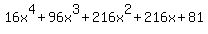 Multiply the terms with their coefficients Multiply the terms with their coefficients
So 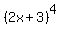 expands and simplifies to expands and simplifies to 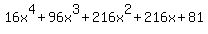 . .
In other words, 
|
|
|