SOLUTION: if p and q are the zeroes of a polynomial ax2+bx+c then evaluate p-q

 where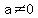 

The sum of the zeros is 

The product of the zeros is 

We will assume the maximal zero is p and the minimal zero is q,
so that p-q will be non-negative, though it may be zero.

We notice that the square of the sum of the zeros has similar terms
to the square of the difference. Notice that:

 is very much like 

except that the first has a 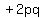 term whereas the second has 
a  term.  

To get an expression for 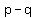 we start with this:



Let's create the square of the sum of the zeros under the
radical by adding and then subtracting the term ,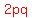
which does not change the value since this amounts to adding 0.



Swapping two of the terms under the radical:



Factoring the first three terms under the radical and combining the
last two terms:



Now since  we substitute  for 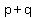 and

and since  we substitute  for :





We get a common denominator of  under the radical, so
we multiply the second term under the radical by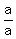 





Combine the fractions over the LCD:



Taking square roots of numerator and denominator:



Since  may be negative, we must use absolute value of a,
since p-q is non-negative:



Edwin