SOLUTION: Solve the equation 4sin(2theta)-3cos=0 for all values on the interval {{{"0°"<=theta<"360°"}}}. Express any non-integer answers to the nearest tenth of a degree.

You left off the angle for the cosine, so I can't tell whether
you meant the equation to be this: 

 

or this:



So I'll do it both ways:

-----------------------------

If it is the first way,



Use the identity 





Factor out 



Use the zero-factor principle.

Set the first factor = 0:



The only angles between 0° and 360° which have their
cosine equaling to zero are 90° and 270°.  So those
are two of the solutions.

Set the second factor = 0:







With a calculator we find the inverse sine of 
is the first quadrant angle 22.02431284°.  However the
angle in the second quadrant whioch has 22.02431284° as
its reference angle is 157.9756872°.

So the four solutions on the interval ,
with the decimals rounded to the nearest tenth of a degree are:

, , ,  

------------------------

If it was supposed to have been the second way:





Divide both sides by 



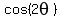
Divide both sides by 4:



Use the identity 



With a calculator we find the inverse tangent of 
is the first quadrant angle 36.86989765°.  However the
angle in the third quadrant which has 36.86989765° as
its reference angle is 216.8698976°.

Now since the angle is 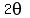 and not just ,
we must find all solutions for 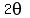 in twice the interval, 
that is the interval , so that 
will be in the interval .   

So we must add 360° to each of those two values, so that when
we find  by dividing by 2 we will have all the
solutions in the interval .

So we have

, , , ,

Now solving for , we have:

, , , ,

Or rounded to the nearest tenth of a degree:

, , , .

Edwin