SOLUTION: The number of positive integers less than or equal to 1501 that are multiples of 3 or 4 but not a multiple of 5 is: (A)875 (B) 850 (C) 750 (D) 725 (E) none of these

We will use these two facts:

1. The number of multiples of k which are less than or equal to n is
given by the greatest integer not exceeding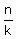 

and

2. N(A or B) = N(A) + N(B) - N(A and B)

--------------------------

First we calculate the number of multiples of 3 or 4.

N(multiples of 3 OR 4) = 

N(multiples of 3) + N(multiples of 4) - N(multiples of 3 AND 4)

The number of multiples of 3 which are less than or equal to 1501
is the greatest integer not exceeding  which is 500.

The number of multiples of 4 which are less than or equal to 1501 is 
the greatest integer not exceeding  which is 375.

The number of multiples of 3 AND 4 which are less than or equal to 1501
is the number of multiples of 12 which are less than or equal to 1501, 
which is the greatest integer not exceeding  which 
is 125.

N(multiples of 3 OR 4) = 

N(multiples of 3) + N(multiples of 4) - N(multiples of 3 AND 4)

N(multiples of 3 OR 4) = 500 + 375 - 125 = 750.

----------------

Now that 750 includes every multiple of 5 less than 1501 which is 
either a multiple of 4 or a multiple of 3.   

So we must count the number of multiples of 15 OR 20 to subtract
from it.

N(multiples of 15 OR 20) = 

N(multiples of 15) + N(multiples of 20) - N(multiples of 15 AND 20)

The number of multiples of 15 which are less than or equal to 1501 
is the greatest integer not exceeding  which 
is 100.

The number of multiples of 20 which are less than or equal to 1501 
is the greatest integer not exceeding  which is 
75.

The number of multiples of both 15 AND 20 which are less than or 
equal to 1501 is the number of multiples of 60 which are less than 
or equal to 1501, which is the greatest integer not exceeding
 which is 25.

N(multiples of 15 OR 20) = 

N(multiples of 15) + N(multiples of 20) - N(multiples of 15 AND 20)

N(multiples of 15 OR 20) = 100 + 75 - 25 = 150.

----------------------------

So we subtract the 150 from the 750, and get 600.

So the correct answer is 600, which is not listed as a choice,
so the correct choice is "(E) none of these".

Edwin