SOLUTION: what are the slopes of the asymptotes of the hyperbola with equation {{{4x^2-y^2+8x-6y=9}}}

First get it in standard form, which is either

 if the hyperbola opens right and left, 

and the slopes of the asymptotes are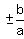 

or

 if the hyperbola opens upward and downward.

and the slopes of the asymptotes are 





Get the  term next to the  term.
Get the  term next to the  term.



Factor the coefficient of  out of the 
first two terms on the left. 
Farctor the coefficient of  out of the 
last two terms on the left. 



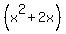Complete the square on  by multiplying
the coefficient of x, which is 2 by  getting 1,
and then squaring 1, getting 1.  And we add that inside the
first parentheses.  However since there is a 4 in fromt of the
first parentheses, adding 1 inside the parentheses amounts
to adding 4*1 or 4 to the left side, so we must add 4 
to the right side:




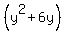Complete the square on  by multiplying
the coefficient of y, which is 6 by  getting 3,
and then squaring 3, getting 9.  And we add that inside the
second parentheses.  However since there is a -1 in fromt of the
second parentheses, adding 9 inside the parentheses amounts
to adding 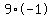 or -9 to the left side, so we must add -9 
to the right side:



Factor the parentheses as squares of binomials, and combine
the numbers on the right:



Get a 1 on the right by dividing through by 4





Since the variable x comes first in the standard form, the
hyperbola opens right and left.

So we compare that to:



The center is at (-1,-3).  So we plot the center:



 so , the semi-transverse axis is 1 unit
long, so we draw the complete transverse axis right and left
1 unit from the center, that is, the tranverse axis is the 
horizontal green line below:

 

 so , the semi-conjugate axis is 2 units
long, so we draw the complete conjugate axis up and down
2 units from the center, that is, the conjugate axis is the 
vertical green line below:

 

Now we draw in the defining rectangle

 

Now we can draw the asymptotes which are the extended diagonals
of the defining rectangle:

 

and we can sketch in the hyperbola:

 

The slopes of the asymptotes are 

Edwin