SOLUTION: Can you please find two examples of prime polynomials? Given a polynomial such as x^2 + 4x + 8 how would I decide if this is factorable or not? What logic would you use to co

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: Can you please find two examples of prime polynomials? Given a polynomial such as x^2 + 4x + 8 how would I decide if this is factorable or not? What logic would you use to co      Log On


   

Question 280572: Can you please find two examples of prime polynomials?
Given a polynomial such as x^2 + 4x + 8 how would I decide if this is factorable or not? What logic would you use to come up with your answer? What about a more complicated polynomial such as 3x^2 + 12x + 4? How would you decide if this is prime or not?
Answer by richwmiller(17219) About Me  (Show Source):
You can put this solution on YOUR website!
Neither of your equations are factorable even though this solver might say they are. This solver considers all real numbers factorable, whereas we normally only consider the equations factorable if there are whole numbers in the factors.
use the quadratic formula
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B4x%2B8+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%284%29%5E2-4%2A1%2A8=-16.

The discriminant -16 is less than zero. That means that there are no solutions among real numbers.

If you are a student of advanced school algebra and are aware about imaginary numbers, read on.


In the field of imaginary numbers, the square root of -16 is + or - sqrt%28+16%29+=+4.

The solution is x%5B12%5D+=+%28-4%2B-+i%2Asqrt%28+-16+%29%29%2F2%5C1+=++%28-4%2B-+i%2A4%29%2F2%5C1+

Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B4%2Ax%2B8+%29

Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 3x%5E2%2B12x%2B4+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%2812%29%5E2-4%2A3%2A4=96.

Discriminant d=96 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-12%2B-sqrt%28+96+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%2812%29%2Bsqrt%28+96+%29%29%2F2%5C3+=+-0.367006838144548
x%5B2%5D+=+%28-%2812%29-sqrt%28+96+%29%29%2F2%5C3+=+-3.63299316185545

Quadratic expression 3x%5E2%2B12x%2B4 can be factored:
3x%5E2%2B12x%2B4+=+3%28x--0.367006838144548%29%2A%28x--3.63299316185545%29
Again, the answer is: -0.367006838144548, -3.63299316185545. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+3%2Ax%5E2%2B12%2Ax%2B4+%29

Solved by pluggable solver: Factoring using the AC method (Factor by Grouping)


Looking at the expression 3x%5E2%2B12x%2B4, we can see that the first coefficient is 3, the second coefficient is 12, and the last term is 4.



Now multiply the first coefficient 3 by the last term 4 to get %283%29%284%29=12.



Now the question is: what two whole numbers multiply to 12 (the previous product) and add to the second coefficient 12?



To find these two numbers, we need to list all of the factors of 12 (the previous product).



Factors of 12:

1,2,3,4,6,12

-1,-2,-3,-4,-6,-12



Note: list the negative of each factor. This will allow us to find all possible combinations.



These factors pair up and multiply to 12.

1*12 = 12
2*6 = 12
3*4 = 12
(-1)*(-12) = 12
(-2)*(-6) = 12
(-3)*(-4) = 12


Now let's add up each pair of factors to see if one pair adds to the middle coefficient 12:



First NumberSecond NumberSum
1121+12=13
262+6=8
343+4=7
-1-12-1+(-12)=-13
-2-6-2+(-6)=-8
-3-4-3+(-4)=-7




From the table, we can see that there are no pairs of numbers which add to 12. So 3x%5E2%2B12x%2B4 cannot be factored.



===============================================================





Answer:



So 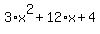3%2Ax%5E2%2B12%2Ax%2B4 doesn't factor at all (over the rational numbers).



So 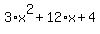3%2Ax%5E2%2B12%2Ax%2B4 is prime.