Question 280538: Consider the following. Three years after purchase a certain car was valued at $16,200. After 7 years the car was valued at $13,800. Assume that the car depreciates in value in a linear manner. Predict the value of the car 10 years after purchase and compute the property tax that one will have to pay on the car at that time if the mill rate is 18.0 and is applied to the value of the car at that time.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! to solve your problem, I had to figure out what mill rate means.
Here's a link to a definition.
http://en.wikipedia.org/wiki/Property_tax
The car is valued at $16,200 3 years after purchase.
The care is valued at $13,800 7 years after purchase.
If we let x = the number of years after purchase, and we let y = the value of the car after x years of purchase, then we have 2 points from which we can draw a straight line and generate an equation for that line.
our points are:
(x1,y1) = (3,16200)
(x2,y2) = 7,13800)
the general form of the slope-intercept form of an equation for a straight line is:
y = mx + b where m is the slope and b is the y-intercept.
First we find the slope:
slope is equal to (y2-y1)/(x2-x1).
This becomes:
m = (13800 - 16200)/(7-3) = -2400 / 4 = -600
The car is depreciating at the rate of $600 per year.
our equation becomes:
y = -600*x + b
Next we need to find the y-intercept.
That's the value of y when x = 0.
To do that, we pick any one of the points on the line.
we could pick (x1,y1) or we can pick (x2,y2).
Either point will yield the same answer for b.
We'll use (x1,y1) = (3,16200)
Our equation of y = -600*x + b becomes 16200 = -600*3 + b which becomes 16200 = -1800 + b.
We add 1800 to both sides of this equation to get:
16200 + 1800 = b which becomes 18000 = b.
Our equation becomes:
y = -600*x + 18000
Now that we have the equation, we can predict the value of the car at the end of 10 years.
We replace x with 10 to get:
y = -600*10 + 18000 which becomes y = -6000 + 18000 which becomes y = 12000.
The car will be worth 12000 at the end of 10 years.
Now we apply the mill rate to that.
A mill rate of 18 means the car will be assessed 18 dollars per thousand dollars of value which would equal a property tax of 18 * 12000 / 1000 = $216 when the car is 10 years old.
A graph of the equation for the value of the car is shown below:
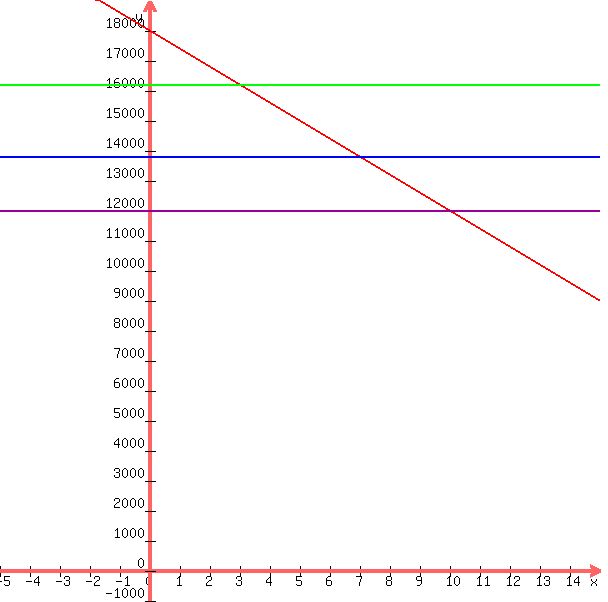
Horizontal lines have been placed at 16200, 13800, and 12000 to show you that these values occur at 3 years, 7 years, and 10 years respectively.
Just drop a perpendicular line from the intersection of the graph of the equation with these horizontal lines to see that the value of x at those intersections is about where it should be: 3 years for 16200, 7 years for 13800, and 10 years for 12000.
|
|
|