Question 280456: form a polynomial f(x) with real coefficients having the given degree and zeros.
degree: 4; zeros: -1, 2, and 1-2i.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! A polynomial of real coefficients will have as many zeros as the degree of the polynomial. Also, any complex zeros will come in conjugate pairs. So if 1-2i is a zero, then 1+2i will also be a zero. So your 4th degree polynomial will have zeros of -1, 2, 1-2i and 1+2i.
If z is a zero of a polynomial, then (x-z) is a factor of the polynomial. So
f(x) = (x-(-1))(x-2)(x -(1-2i))(x - (1+2i))
All we have to do is simplify this. We can start by simplifying the expressions for each factor:
f(x) = (x+1)(x-2)(x-1+2i)(x-1-2i))
Now to multiply the factors. I'll start with the easy part, multiplying the first two factors:

Now I'll multiply the last two factors. If we notice the pattern of the factors the multiplication is actually fairly easy. In case you have trouble seeing the pattern, am going to use some temporary variables:
Let a = x-1
and b = 2i
Now the last two factors are
(a+b)(a-b)
which, we should know, results in
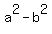
Replacing the temporary variables we now have:

Simplifying we get:




(Note: If you still don't see how the pattern helped us multiply (x-1+2i)(x-1-2i), then just multiply it out the long way. You should still end up with 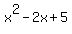 .) .)
Now we have just one more multiplication. We multiply each term of the first factor by each term of the second factor:

Combining the like terms we get:

which is the 4th degree polynomial with the specified roots.
|
|
|