SOLUTION: find the equation, in standard form, of the parabola {{{3y^2+6y-x+6=0}}}

Standard form is



Get the y-terms on the left and the others on the right:





Divide through by 3, the coefficient of :



Complete the square on the left:

1. Multiply the coefficient of y, which is 2 by , getting 1
2. Square 1, getting 1
3. Add 1 to both sides:



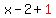Factor the left side as a perfect square, combine terms on the right.



Factor out , the coefficient of x on the right,
by dividing the  by  like this:  


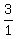
So we have the standard form:



Edwin