SOLUTION: Given Function and one of its zeros, find all of the zeros of the function. h(x)={{{x^3-11x+20;2+i}}}

Algebra ->  Rational-functions -> SOLUTION: Given Function and one of its zeros, find all of the zeros of the function. h(x)={{{x^3-11x+20;2+i}}}      Log On


   

Question 279410: Given Function and one of its zeros, find all of the zeros of the function.
h(x)=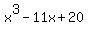x%5E3-11x%2B20%3B2%2Bi
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
Given Function and one of its zeros, find all of the zeros of the function.
h(x)=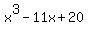x%5E3-11x%2B20%3B2%2Bi
----------------------------
20 has factors of 1, 2, 4, and 5 to consider
Because of the 11x, it has to be an even number, so 1 and 5 are out.
Try 2 and 4, plus and minus
h(2) = not zero
h(4) is too big
h(-4) = 0 That's one.
------------
Divide by (x+4)
--> x%5E2+-+4x+%2B+5+=+0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B-4x%2B5+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-4%29%5E2-4%2A1%2A5=-4.

The discriminant -4 is less than zero. That means that there are no solutions among real numbers.

If you are a student of advanced school algebra and are aware about imaginary numbers, read on.


In the field of imaginary numbers, the square root of -4 is + or - sqrt%28+4%29+=+2.

The solution is x%5B12%5D+=+%28--4%2B-i%2Asqrt%28+-4+%29%29%2F2%5C1+=++%28--4%2B-i%2A2%29%2F2%5C1+, or
Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-4%2Ax%2B5+%29

--------------
x = 2 ± i