|
Question 278156: (8x^3-4x^2-6x-36)/(x-4) Thanks for your help.
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!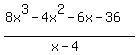 
Since this fraction does not simplify. I'm guessing that the actual fraction is:
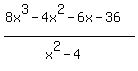
Simplifying fractions involves canceling factors that are common to the nnumerator and denominator. To cancel factors we need factors.
So we start by factoring. The numerator has a GCF of 2 which we can factor out. And the denominator is a difference of squares so it factors easily.
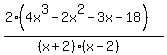
We don't have common factors yet so we keep factoring.
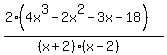
The second factor in the numerator- doesn't fit any of the factoring patterns
- has too many terms for trinomial factoring
- doesn't appear to be factorable by grouping.
So it seem that we need to factor by trial and error of the possible rational roots. The possible rational roots are the ratios, positive and negative, which can be formed using a factor of the constant term (at the end, 18 in your case) over a factor of the leading coefficient, 4. The factors of 18 are 1, 2, 3, 6, 9 and 18. The factors of 4 are 1, 2 and 4. So there are a lot of possible rational roots. But we're only interested in factors that match a factor in the denominator. So the only roots worth trying here are 2 and -2. I'm going to try 2 first. To check a rational root is probably easiest with synthetic division:
2 | 4 -2 -3 -18
8 12 18
---------------
4 -6 9 0
The remainder is zero so 2 is a rational root and (x-2) is a factor. And, from the numbers in front of the remainder, the other factor is 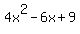 . So now our factored fraction is:
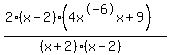
We could try to continue to factor the numerator but we can see that the rational roots of 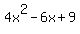do not include -2. So x+2 will not be a factor. Since any other factors do not help we won't bother factoring any more. Now we can cancel the common factor of x-2:
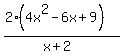
which simplifies to:
|
|
|
| |
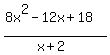
