|
Question 278152: Not sure where to start with this one:
An orchard contains 30 apple trees, each of which yields approx 400 apples over the growing season. The owner plans to add more trees, but the guys at Texas A&M advise that b/c of crowding, each new tree will reduce the average yield per tree by about 10 apples over the growing season. How many trees should be added to maximize the total yield of apples, and whit is the maximum yield?
x=30
y=400 I think, but how do I plug this into a quadratic function? Or is that even the direction I need to go?
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let x = number of new trees to be planted.
So adding 'x' trees to the already established 30 trees gives us 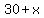 trees total. Now because "each new tree will reduce the average yield per tree by about 10 apples over the growing season", this means that each tree will produce trees total. Now because "each new tree will reduce the average yield per tree by about 10 apples over the growing season", this means that each tree will produce  apples. To see why, let x=1 which means that 400-10(1)=400-10=390. So planting one new tree means that each tree only produces 390 apples, which is what we expect. Try other values of 'x' to confirm this expression. apples. To see why, let x=1 which means that 400-10(1)=400-10=390. So planting one new tree means that each tree only produces 390 apples, which is what we expect. Try other values of 'x' to confirm this expression.
Since we have 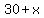 trees which each produce trees which each produce  apples, this means that there will be a total of apples, this means that there will be a total of 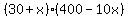 apples total after 'x' trees are planted. apples total after 'x' trees are planted.
Note: if there is a part that doesn't make sense explained above, it is wise to go over it again or ask me about it. Translation is a critical element to solving word problems.
So let 
 Start with the given equation. Start with the given equation.
 FOIL FOIL
 Rearrange and combine like terms. Rearrange and combine like terms.
Now the goal is to maximize 'y' which is the total number of apples. To do this, we need to find the y coordinate of the vertex. Remember that the vertex is the highest/lowest point on a graph. In this case, it is the highest point on the parabola.
In order to find the vertex, we first need to find the x-coordinate of the vertex.
To find the x-coordinate of the vertex, use this formula:  . .
 Start with the given formula. Start with the given formula.
From  , we can see that , we can see that  , ,  , and , and  . .
 Plug in Plug in  and and  . .
 Multiply 2 and Multiply 2 and  to get to get  . .
 Divide. Divide.
So the x-coordinate of the vertex is  . Note: this means that the axis of symmetry is also . Note: this means that the axis of symmetry is also  . .
Now that we know the x-coordinate of the vertex, we can use it to find the y-coordinate of the vertex.
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Square Square  to get to get  . .
 Multiply Multiply  and and  to get to get  . .
 Multiply Multiply  and and  to get to get  . .
 Combine like terms. Combine like terms.
So the y-coordinate of the vertex is  . .
So the vertex is ) . .
Since the y-coordinate of the vertex is  , this means that the maximum production of apples is 12,250 which occurs when 5 new trees are planted (since x=5 at the vertex). , this means that the maximum production of apples is 12,250 which occurs when 5 new trees are planted (since x=5 at the vertex).
|
|
|
| |