Question 27663: Perform the indicated divisions.
8x^3 - 6x^2 + 2x
________________
4x + 1
I am no good at this.
I appreciate your help. Thank you.
Answer by longjonsilver(2297)   (Show Source): (Show Source):
You can put this solution on YOUR website! ok... long division:
in dividing 2345 by 18, you consider how many 18's go into "2"-000: Answer none.
Now, we extend to think of as "23"-00
--> 18's in 23? answer 1 with 5 left over.
So, now how many 18's go into 545.
--> How many 18's into 5? Answer: zero
Now we extend again
--> how many 18's into 54? answer 3 with no remainder.
And the final 5? that is the final remainder.
--> Complete Answer is 103 and 5/18
We do the exact same process with algebraic expressions.
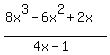
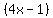
How many 4x's go into 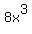 ? Answer is ? Answer is  . .
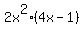 is is  so subtract that from the original, leaving us with so subtract that from the original, leaving us with 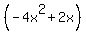 --> call this the "new original" --> call this the "new original"
Now repeat the process...
How many times does 4x go into 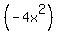
Answer is -x.
So, 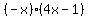 is is 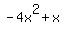 . Now subtract that from the "new original", leaving us with x --> call this the "new original". . Now subtract that from the "new original", leaving us with x --> call this the "new original".
Now repeat the process again...
How many times does 4x go into x
Answer is (1/4).
So  is is 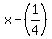 . Now subtract this from the "new original", leaving us with (1/4). . Now subtract this from the "new original", leaving us with (1/4).
This is the end.
Answer to 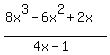 is is 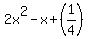 with remainder (1/4). with remainder (1/4).
The secret is to put the working out under itself, in neat columns, so you can see it all. I cannot do that here :-( However, this website
http://www.rfbarrow.btinternet.co.uk/htmasa2/AlgDiv1.htm
shows the process perfectly.
jon.
|
|
|