First let's learn where the Pythagorean identities came from,
namely the Pythagorean theorem:
 By the Pythagorean theorem:
By the Pythagorean theorem:
 Divide through by
Divide through by 


 That's the first Pythagorean identity:
-------------------------------------
That's the first Pythagorean identity:
-------------------------------------
 Divide through by
Divide through by 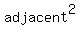


 That's the second Pythagorean identity:
-------------------------------------
That's the second Pythagorean identity:
-------------------------------------
 Divide through by
Divide through by 


 That's the third Pythagorean identity:
-------------------------------------
Be sure to memorize all three of them. Usually we write them
this way, so they're easier to learn:
That's the third Pythagorean identity:
-------------------------------------
Be sure to memorize all three of them. Usually we write them
this way, so they're easier to learn:


 --------------------------------------
Those identities are true for ALL angles
--------------------------------------
Those identities are true for ALL angles  So for
So for
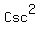
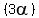

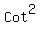
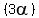 Since the third Pythagorean identity
Since the third Pythagorean identity
 is true for ALL angles
is true for ALL angles  , let
, let  , then
, then
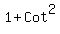
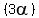

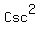
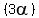 So we can replace
So we can replace 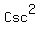
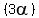 by
by 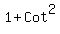
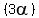 So your problem:
So your problem:
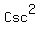
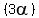

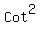
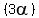 becomes:
becomes:
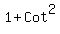
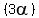

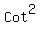
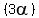 then the "cotangent squared"s cancel:
then the "cotangent squared"s cancel:
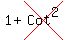

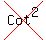
 and that just leaves 1, which is an integer.
Edwin
and that just leaves 1, which is an integer.
Edwin