Question 276215: log10S=0.425 log10W+.725 log10H+log10 71.8
Use the properties of logarithms to write a formula for S without logarithms
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! Since a 10 follows "log" in each term, I'm assuming that the "10" is the base of each logarithm. If the 10's are part of the argument, I will show you a solution for this at the end.
In the meantime, since it is optional to write the base when the base is 10, I will omit the base:
To eliminate logarithms from an equation (without using decimal approximations), there are three ways I can think of at the moment:- Some logarithms can be simplfied "by hand". For example,
 ,  ,  . So these logarithms can be replaced with their simplified, non-logarithmic equivalents. - For equations of the form:
log(expression) = other-expression
we can eliminate the logarithm by rewriting it in exponential form. For example
can be rewritten as:
 (which has no logarithms) - For equations of the form:
log(expression) = log(other-expression)
we can eliminate both logarithms. Logarithms, as I hope you know, represent the exponent for the base which results in the argument. For example, 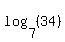 represents the exponent for 7 which results in 34.
The equation above says that two logarithms are equal. More specifically, two exponents are equal. Regardless of the base, if the same exponent for the same base results in both expressions then the expressions must be the same! So we can rewrite
log(expression) = log(other-expression)
as
expression = other-expression
Since there are variables in the arguments of the first 3 logarithms and since the power of 10 which results in 71.8 can't be found "by hand", the first method of eliminating logarithms will not work here. So we looking to change the equation so that it fits one of the forms in the other two methods. Since every term in your equation has a logarithm, we will aim for the third, "all-logarithm" form:
log(expression) = log(other-expression)
This form requires a single logarithm on each side. Somehow we need to combine the three logarithms on the right into one. These three logarithms are not like terms so we cannot add them together into a single logarithm. Fortunately there is a property we can use:
which allows us to combine two logarithms which have the same base and which have a "+" between them. But the property requires that the two logarithms have no (visible) numbers in front of them. (In other words, the coefficients must be 1's.)
Two of the three logarithms have coefficients other than 1. Somehow we need to change these coefficients before we can use the property to combine the logarithms. Another property of logarithms,  , comes to the rescue. It allows us to move the coefficient of a logarithm into the argument as an exponent.
So we will start by moving the coefficients into the arguments:
Now we will use the other property to combine these logarithms. (I hope it is not "too much" for me to combine all three at once. If the following is not clear, just combine two of the logarithms into one. And then combine the remaing two logarithms into one. You'll get the same result if you do it right.)
We know have achieved the desired form of:
log(expression) = log(other-expression)
As explained earlier, we can now rewrite this as:
One more thing.... It is common practice to write expressions like the right side with the number in front and the variables in alphabetical order. Using the Commutative Property of Multiplication we can shift the order of the factors:
If the 10's in the original equation were not the bases of the logarithms, then you would solve the problem using the same steps and eventually reach the equation:
Then we would just divide both sides by 10:
|
|
|
