Question 275363: A farmer wishes to build a large rectangular grazing area of dimensions, width, w, and length, l,splitting the area in to 5 equal fields by dividing the width into 5 equal pieces. The total area of all the fields must be 10500 square feet. Find the dimensions that uses the least amount of fencing.
(It is not always the case that the width is shorter than the length. Round-off your answers to 3 decimal places.)
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A farmer wishes to build a large rectangular grazing area of dimensions, width, w, and length, l, splitting the area in to 5 equal fields by dividing the width into 5 equal pieces.
The total area of all the fields must be 10500 square feet.
Find the dimensions that uses the least amount of fencing.
:
Perimeter:
P = 6L + 2W
:
Area:
L * W = 10500
W = (10500/L)
:
Substitute in the Perimeter equation
P = 6L + 2(10500/L)
:
Plot this equation as: y = (21000/x) + 6x, y=perimeter, x=Length
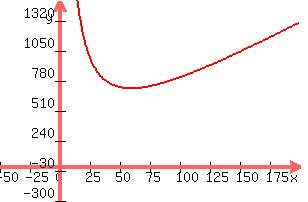
:
Minimum occurs at 59.16 ft for the length (found on a graphing calc)
width: 10500/59.16 = 177.5 ft
Perimeter = 710 ft
;
:
Check this: 6(59.16) + 2(177.5) = 709.9 ~ 710 ft
|
|
|