Question 274948: . factor and find all complex 0's for f(x)=x^4+3x^2-8x^2-22x-24
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
The zeros of a function are the values of x that make the value of the polynomial zero. To find the zeros of a polynomial of degree 3 or more, factor it.
Of all the factoring techniques (GCF, patterns, trinomial, grouping and trial and error of rational roots) the only one I can see that will work on this polynomial is trial and error of the rational roots.
The possible rational roots of a polynomial are all the possible numbers, positive and negative, formed by making a fraction where the numerator is a factor of the constant term (at the end) and the denominator is a factor of the leading coefficient.
Since the leading coefficient is 1, all the denominators of the rational roots will be 1's. This means they will all be integers. The constant term at the end is -24 (although the "-" is not significant here). So the possible rational roots are 1, 2, 3, 4, 6, 8, 12 and 24 (both positive and negative). This is 16 possible rational roots. It can take a while to find the roots (which is why this is this method is my method of last resort).
The easiest way to test for roots is synthetic division (which I hope you already know). This is a trial and error method. It took me 5 attempts before I found 1 that worked:
3 | 1 3 -8 -22 -24
--- 3 18 30 24
--------------------
1 6 10 8 0
With the remainder is zero, it means 3 is a root and (x-3) is a factor. The numbers preceding the remainder on the bottom line tell you the other factor. So now we know:

With f(x) being a 4th degree polynomial, there will be 4 roots. So far we have 1. So we continue but now we are looking for roots of the second factor. This means our list of possible roots has shortened to 1, 2, 4 and 8 (positive and negative). And, if we're clever, we'll realize that none of the positive roots could work on the polynomial 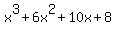 . This is so because we have to have some positive and some negative numbers in order to add up to zero. And if x is positive and all the coefficients are positive like they are in . This is so because we have to have some positive and some negative numbers in order to add up to zero. And if x is positive and all the coefficients are positive like they are in 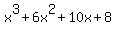 none of the terms will ever be negative. So at this point I knew that only only possible roots were -1, -2, -4 or -8. (Note: If you tried any of these numbers earlier with f(x) and they did not work, they will not work here, either. So don't try any of the possible roots more than once.). Since my earlier attempts included -1 and -2 I tried -4 next: none of the terms will ever be negative. So at this point I knew that only only possible roots were -1, -2, -4 or -8. (Note: If you tried any of these numbers earlier with f(x) and they did not work, they will not work here, either. So don't try any of the possible roots more than once.). Since my earlier attempts included -1 and -2 I tried -4 next:
-4 | 1 6 10 8
---- -4 -8 -8
-------------
1 2 2 0
So -4 is another root and (x - (-4)) or (x+4) is a factor:

Two more roots to go. The third factor above is a 2nd degree (or quadratic) polynomial. We could continue to try the possible rational roots but we have other options. There are other factoring techniques that could work on this, patterns or trinomials, and we also have the option of using the Quadratic Formula. Since I can see that the factoring will not work, I'll use the quadratic formula:

Simplifying:



With a negative number inside the square root we are going to end up with a pair of complex roots.



Factoring out 2 in the numerator:

The 2's cancel:

So our 4 zeros/roots are: 3, -4, -1+i, -1-i
|
|
|