Question 274722: Hi, pls help me find derivative of following:
1. f(x) =16x+19, find f'(8)=?
2. if f(x)= 2e^(x+1) + e^1, then f'(0) = ?
2. g(x)=(e^x)/(1+3x), find g'(x)=?
4. if f(t)= sq.root of 5/t^7, find f'(t)=?
Thank you,
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! We'll need the following to solve your problems:In each of the these, c and n are constants and f, g, u and v are functions- if f(x) = c then f'(x) = 0
- if f = x then f' = 1
- if f = c*g then f' = c*g'
- if f = u + v then f' = u' + v'
- if
 then f' = then f' = 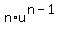 *u'. Rule 5a: if *u'. Rule 5a: if  , then f' = , then f' = 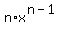 - if f = u/v then f' = (v*u' - u*v')/v^2
- if
 then f' = u'* then f' = u'*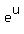
To find derivatives you need to learn how to take a function and figure out how to express it in the form of one or more of the rules for derivatives. (Note: I've only listed the ones we need for these problems. There are more.)
1. f(x) =16x+19, find f'(8)=?
Let u(x) = 16x and v(x) = 19, which makes f = u + v. Then by rule #4:
f' = u' + v'
By rule #1 v' = 0 so now
f' = u'
For u', let c = 16 and g(x) = x. By rule #3 u' = c*g' so now
f' = 16*g'
From rule #2, g' = 1 so now
f' = 16*1 = 16
Since f' is a constant, f'(anything, including 8) = 16
I hope this makes sense. After all, f(x) is a line with a (constant) slope of 16 and first derivatives are formulas for slope. We will used this in the problems that follow. For any function that is a line we will just use the coefficient of x (the slope) for the derivative instead of working through all these rules for derivatives.
2. if  , then f'(0) = ? , then f'(0) = ?
Let  and and  which makes f = u + v. By rule #4: which makes f = u + v. By rule #4:
f' = u' + v'
Since v(x) is a constant (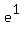 is simply a number, after all.) then v' = 0 (rule #1) so now is simply a number, after all.) then v' = 0 (rule #1) so now
f' = u'
Let c = 2 and  which makes u = c*g. By rule #3, u' = c*g' so now which makes u = c*g. By rule #3, u' = c*g' so now
f' = 2*g'
Let h(x) = x+1 which makes  . By rule #7 g' = h'* . By rule #7 g' = h'*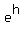 . Since h is a line, h' is the slope of that line: 1 which means g' = . Since h is a line, h' is the slope of that line: 1 which means g' = 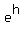 . So now . So now
f' = 
f'(0) = 
3.  , find g'(x)=? , find g'(x)=?
Let u(x) =  and v(x) = 1+3x which makes g = u/v. By rule #6 and v(x) = 1+3x which makes g = u/v. By rule #6
g' = (v*u' - u*v')/v^2
By rules 7 and 2, u' =  . And since v is a line, v' is the slope of that line: 3. So now . And since v is a line, v' is the slope of that line: 3. So now
g'(x) = 
4. if  , find f'(t)=? , find f'(t)=?
To make this one a little easier I'm going to rewrite f(t) using exponents:

(This was not necessary but it does make the derivative much simpler.)
Let c =  and and  then by rule #3 then by rule #3
f' = c*g'
By rule #5a, g' =  . This makes . This makes
f'(t) = 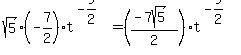
|
|
|