Question 274623: I know to find roots, but am not sure why this problem wont turn out.
Find all roots of the equation:
x to the fourth plus three x to the third subtract x squared plus nine x subtract twelve equals zero.
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
To find the roots we need to factor this. The Greatest Common Factor (GCF) is 1 (which we rarely bother factoring out). This expression has too many terms for any of the commonly used patterns and it has too many terms for factoring trinomials. And I don't see how factoring by grouping would work. So we are left with factoring by trial and error of the possible rational roots.
Trial and error can be tedious, especially if there are a lot of possible rational roots. The possible rational roots are all the positive and negative numbers which can be formed using a factor of the constant term (the number without a variable at the end) in the numerator and a factor of the leading coefficient in the denominator.
Your polynomial has a constant term of -12 and a leading coefficient of 1. So the possible rational roots are: 1, -1, 2, -2, 3, -3, 4, -4, 6, -6, 12, -12. This could take a while. But I will try to explain how to avoid wasting time.
1 is always a possible rational root (because it is a factor of every constant term and leading coefficient) and it is easy to check mentally. Just add all the coefficients (since 1 to any power is 1 the exponents don't really matter after all. If the sum is 0 then 1 is a root.
Your coefficients are: 1 3 -1 9 and -12. If you add these up you find that the sum is 0!! So we know that 1 is a root. And if 1 is a root, then x-1 is a factor of your polynomial. We can use synthetic division to divide by x-1 and find the other factor:
1 | 1 3 -1 9 -12
--- 1 4 3 12
-----------------
1 4 3 12 0
So 
We could continue to try other rational roots. If you do, then- Find rational roots of the second factor above.
- Do not bother trying any positive roots. There are no other positive rational roots. I can say this because
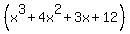 has coefficients that are all positive. And if both the coefficients and x are positive, how can 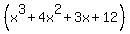ever be zero? Answer: It can't. We have to get some negatives from somewhere in oder for it to add up to zero.
However, instead of trying more rational roots, I'm going to use factoring by grouping to finish the factoring:
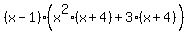
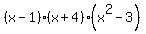
So
From this we can see that the rational roots are 1 and -4. And there two imaginary roots:  and 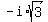 . (If you don't see these roots, take each factor, set it equal to zero and solve.)
|
|
|
