SOLUTION: Rationalize denomiators, Assume all expressions under radicals represent positive numbers. ∛(3y^4 )/∛(6x^4 )

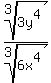First write all as one cube root:



Cancel the 3 into the 6, leaving 2 on the bottom:



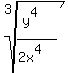Now we must multiply the denominator by whatever is necessary
to make it into a perfect cube.  The  needs to be multiplied
by 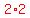 or  to make it become 
which is a perfect cube. The  needs to be multiplied by 
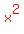 to make it become  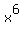which is a perfect cube.

So to make the denominator become a perfect cube, we need to
multiply it by .

Howver to keep from changing the value when we multiply the
denominator by something, we have to multiply the numerator
by the same quantity, so we multiply both numerator and denominator
by , and then



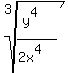becomes:





Now you can take the cube root in the denominator, leaving it
rationalized, that is, with no irrational radical at all. All
you do is divide the exponents by the radical index 3:



Change the 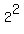 to 4 and erase the 1 exponent in the bottom:



There is still something left you must do.  Write 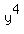 as 
, and then you have:



Now take the cube root of  by putting a y on the
outside of the radical:

 

Edwin