Question 274329: x^2+10x-128. I've had this problem a few times now (I'm a tutor myself) and it asks to solve for x. I just cannot factor this. Please help me refresh my algebra skills and help me find a way to solve for x on this one. Thank you.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! For more factoring help, check out this quadratic formula solver.
| Solved by pluggable solver: Factoring using the AC method (Factor by Grouping) |
Looking at the expression  , we can see that the first coefficient is , we can see that the first coefficient is  , the second coefficient is , the second coefficient is  , and the last term is , and the last term is 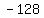 . .
Now multiply the first coefficient  by the last term by the last term 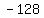 to get to get  . .
Now the question is: what two whole numbers multiply to 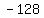 (the previous product) and add to the second coefficient (the previous product) and add to the second coefficient  ? ?
To find these two numbers, we need to list all of the factors of 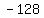 (the previous product). (the previous product).
Factors of 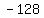 : :
1,2,4,8,16,32,64,128
-1,-2,-4,-8,-16,-32,-64,-128
Note: list the negative of each factor. This will allow us to find all possible combinations.
These factors pair up and multiply to 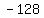 . .
1*(-128) = -128
2*(-64) = -128
4*(-32) = -128
8*(-16) = -128
(-1)*(128) = -128
(-2)*(64) = -128
(-4)*(32) = -128
(-8)*(16) = -128
Now let's add up each pair of factors to see if one pair adds to the middle coefficient  : :
| First Number | Second Number | Sum | | 1 | -128 | 1+(-128)=-127 | | 2 | -64 | 2+(-64)=-62 | | 4 | -32 | 4+(-32)=-28 | | 8 | -16 | 8+(-16)=-8 | | -1 | 128 | -1+128=127 | | -2 | 64 | -2+64=62 | | -4 | 32 | -4+32=28 | | -8 | 16 | -8+16=8 |
From the table, we can see that there are no pairs of numbers which add to  . So . So  cannot be factored. cannot be factored.
===============================================================
Answer:
So  doesn't factor at all (over the rational numbers). doesn't factor at all (over the rational numbers).
So  is prime. is prime.
|
So you must use the quadratic formula
So let's use the quadratic formula to solve 
For more help with the quadratic formula, check out this quadratic formula solver.
| Solved by pluggable solver: Quadratic Formula |
Let's use the quadratic formula to solve for x:
Starting with the general quadratic

the general solution using the quadratic equation is:

So lets solve  ( notice ( notice  , ,  , and , and  ) )
 Plug in a=1, b=10, and c=-128 Plug in a=1, b=10, and c=-128
 Square 10 to get 100 Square 10 to get 100
 Multiply Multiply  to get to get 
 Combine like terms in the radicand (everything under the square root) Combine like terms in the radicand (everything under the square root)
 Simplify the square root (note: If you need help with simplifying the square root, check out this solver) Simplify the square root (note: If you need help with simplifying the square root, check out this solver)
 Multiply 2 and 1 to get 2 Multiply 2 and 1 to get 2
So now the expression breaks down into two parts
 or or 
Now break up the fraction
 or or 
Simplify
 or or 
So the solutions are:
 or or 
|
|
|
|