Question 27384: Let V = P3(Q) and W = { f(x) 2 V | f(x) = f(−x + 1) }. Find a basis for W.
Let V and W be same as above. Find a basis for V that contains a basis for W.
I am totally confused. I really need some help here.
Thanks.
Answer by khwang(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let V = P3(Q) and W = { f(x) 2 V | f(x) = f(−x + 1) }. Find a basis for W.
Let V and W be same as above. Find a basis for V that contains a basis for W.
[Usually, P3(Q) means the vector space of polynomials of deg <= 3 in Q[x])
Sol: If f(x) =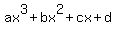 belongs to W , then f(x) = f(-x+1) implies belongs to W , then f(x) = f(-x+1) implies  or or 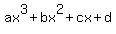 = =  = = 
By comparing the coefficients, we have a=-a, 3a+b = b, -3a-2b-c=c , d= –a+b+c+d. Hence, a= 0, b+c = 0. We see that W = { 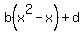 | b,d in Q} (generated by | b,d in Q} (generated by 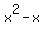 & 1and so dim W = 2. By choosing B’ = {1, & 1and so dim W = 2. By choosing B’ = {1, 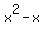 } we get a basis of W. The adjoining two independent vectors } we get a basis of W. The adjoining two independent vectors 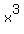 and x (not in W) to B', then we can get a basis B= {1, and x (not in W) to B', then we can get a basis B= {1, 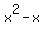 , ,  , x} of V, which contains a basis B’ for W. , x} of V, which contains a basis B’ for W.
Kenny
|
|
|