SOLUTION: Can anyone help me with this question? I am so stumped with this one In most businesses, increasing prices of their product can have a negative effect on the number of custom

Algebra ->  Functions -> SOLUTION: Can anyone help me with this question? I am so stumped with this one In most businesses, increasing prices of their product can have a negative effect on the number of custom      Log On


   

Question 27259: Can anyone help me with this question?
I am so stumped with this one

In most businesses, increasing prices of their product can have a negative effect on the number of customers of the business. A bus company in a small town has an average number of riders of 800 per day. The bus company charges $2.25 for a ride. They conducted a survey of their customers and found that they will lose approximately 40 customers per day for each $.25 increase in fare.
Given the descriptions below, plot a graph of the function, explain your choice, and give the domain and range of the function.

Any help will be greatly appreciated
Thanks in advance
Answer by bmauger(101) About Me  (Show Source):
You can put this solution on YOUR website!
We're looking for a hypothetical increase (or decrease) in bus fair, based on maximizing profit. Since the problem doesn't presume any additional overhead per rider (eg, no matter what happens we won't be adding buses or needing more drivers or any other expense) our profit is purely based on two factor, riders and the fare. To find profit, we multiply the two together. So if 800 riders pay $2.25 each, we'll be making:
800%2A2.25=1800
So far no problem, but we need to be able to see what happens when we change the fair. Let's call the fare increase x. So the new fare will be:
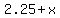
2.25%2Bx
But as the problem says, changing the fair will change the number of riders. Everytime x changes by 25 cents we lose 40 customers. A change of a dollar we'll lose 160 customers (160x).
When you subtract our lost riders from a base of 800:
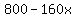
800-160x
We'll now multiply the fare (2.25+x) times the riders (800-160x):
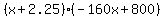
%28x%2B2.25%29%28-160x%2B800%29
Solving graphically:
graph%28+300%2C+200%2C+-2%2C+8%2C+-500%2C+2400%2C+%282.25%2Bx%29%28800-160x%29%29
This shows that we should expect that an optimal fare increase of a little less than $1.50 will gross us the most money, approximately $2000.
Algebraically we want to find the maxima for the graph.
y=%28x%2B2.25%29%28-160x%2B800%29Factor:
y=-160%28x%2B2.25%29%28x-5%29FOIL:
y=160%28x%5E2-2.75x-11.25%29Completing the square:
y%2F160%2B11.25=x%5E2-2.75x%2B121%2F64
y%2F160%2B11.25%2B%28121%2F64%29=%28x-22%2F16%29%5E2Multiply everything by 160:
y%2B1800%2B302.5=160%28x-22%2F16%29%5E2
y%2B2102.5=160%28x-22%2F16%29%5E2
So your optimal fare increase is 22/16, or $1.375 or $2.25+1.375=$3.625. At that rate we'll have 22/16*160 or 220 fewer riders, or 800-220=580 riders. So we'll make 580 x 3.625 = $2102.5 profit. Of course we've got a problem that we have a half a penny to work with, as you can't have a $1.375 fair increase, and it's probably not even practical to have a fair increase that isn't an even nickel. So maybe you'd argue for a fair increase of $1.40 or $1.35 instead. Hope that helps.