Question 272384: Working together, Ethel, Beryl, and Cora can dig a drainage ditch in 3.5 hours. Working alone, Coral can do it in 10 hours, while Ethel can do it 2 hours faster than Beryl. How long will it take Beryl to dig the ditch by herself? (Round your answer to two decimal places.)
Found 2 solutions by scott8148, ankor@dixie-net.com:
Answer by scott8148(6628)   (Show Source): (Show Source):
You can put this solution on YOUR website! (3.5 / 10) + (3.5 / (B - 2)) + (3.5 / B) = 1
3.5 (B - 2) (B) + 3.5 (10) (B) + 3.5 (10) (B-2) = 10 (B) (B - 2)
3.5B^2 - 7B + 35B + 35B - 70 = 10B^2 - 20B
0 = 6.5B^2 - 83B + 70
use quadratic formula to find B
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Working together, Ethel, Beryl, and Cora can dig a drainage ditch in 3.5 hours.
Working alone, Coral can do it in 10 hours, while Ethel can do it 2 hours faster than Beryl.
How long will it take Beryl to dig the ditch by herself? (Round your answer to two decimal places.)
:
Let e = E digging alone
Let b = B alone
Let c = C alone
:
let the completed job = 1
:
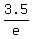 + +  + + 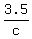 = 1 = 1
:
It says c can do it in 10 hrs, so we have:
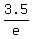 + +  + + 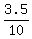 = 1 = 1
:
It also says e = (b-2), so we have
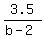 + +  + + 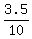 = 1 = 1
Which is
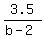 + +  + .35 = 1 + .35 = 1
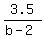 + +  = 1 - .35 = 1 - .35
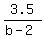 + +  =.65 =.65
:
Multiply equation by: b(b-2); results:
:
b(3.5) + 3.5(b-2) = .65b(b-2)
:
3.5b + 3.5b - 7 = .65b^2 - 1.3b
:
7b - 7 = .65b^2 - 1.3b
Arrange as a quadratic equation
.65b^2 - 1.3b - 7b + 7 = 0
:
.65b^2 - 8.3b + 7 = 0
Solve this using the quadratic equation (a=.65, b=-8.3, c=7)
:
the solution that makes sense: b = 11.86 hrs, B working alone
|
|
|