Question 272255: I am trying to solve this problem, and the answer is in the back of the book, but I keep getting the wrong answer. First for the problem: Tree Density:Ecologists studies the spacing between individual trees in a forest in Britsh Columbia. This lodgepole pine forest was 40 to 50 years old and had approximiately 1600 trees per acre that are randomly spaced. The probablity or liklihood that there is at least one tree located with a radius of x feet is estimated by P(x) =1-e^-0.1144x. For example, P(7)≈0.55 means that if a person picks a point at random in the forest, there is a 55% chance that at least one tree will be located within 7 feet.
a) Evaluate P(2) and P(20), and interpret the results.
b) Graph P. Explain verbally why it is logical for P to be an increasing function. Does the graph have a horizontal asymptote?
c) Solve P(x)=0.5 and interpret the results.
I keep getting the wrong answer. Here is what I came up with. I cannot figure out how to do the graphing part. I have the TI-Nspire, but outside of logs, I mostly use the TI-84 keypad. Here is my workup. 1 Ė e-0.1144x = 0.5
e-0.1144x = 0.5
ln(e-0.1144x) = ln(0.5)
-0.1144x = ln(0.5)
ln(0.5)
x = ---------- = 6.1
0.1144
I got that there is 0.5, or 50%, probability to find another tree in the circle with the radius 6.1 ft around. The actual answer in the back of the book . Here it is word for word.
a) P(2)≈0.20 and P(20) ≈ 0.90. There is a 20% chance that at least one tree is located within a circle having radius 2ft and a 90% chance for a circle having a radius 20 ft.
b) The larger the circle, the more likely it is to contain a tree. Y=1; probability cannot be greater than 1. They then show a graph with a window of [0, 25, 5] by [0, 1, 0]. But, I donít know what to put in for Y1 or any others if needed.
c) x≈6.1. A circle of radius 6.1 ft has a 50-50 chance of containing at least one tree.
Thanks so much.
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! I am trying to solve this problem, and the answer is in the back of the book, but I keep getting the wrong answer.
First for the problem: Tree Density:
Ecologists studies the spacing between individual trees in a forest in Britsh Columbia.
This lodgepole pine forest was 40 to 50 years old and had approximiately 1600 trees per acre that are randomly spaced.
The probablity or liklihood that there is at least one tree located within a radius of x feet is estimated by P(x) =1-e^-0.1144x. For example, P(7)≈0.55 means that if a person picks a point at random in the forest, there is a 55% chance that at least one tree will be located within 7 feet.
a) Evaluate P(2) and P(20), and interpret the results.
b) Graph P. Explain verbally why it is logical for P to be an increasing function. Does the graph have a horizontal asymptote?
c) Solve P(x)=0.5 and interpret the results.
I keep getting the wrong answer. Here is what I came up with. I cannot figure out how to do the graphing part. I have the TI-Nspire, but outside of logs, I mostly use the TI-84 keypad. Here is my workup. 1 Ė e-0.1144x = 0.5
e^(-0.1144x) = 0.5
ln(e-0.1144x) = ln(0.5)
-0.1144x = ln(0.5)
x = [ln(0.5)]/(-0.1144)
---
x = 6.1
I got that there is 0.5, or 50%, probability to find another tree in the circle with the radius 6.1 ft around. The actual answer in the back of the book . Here it is word for word.
a) P(2)≈0.20 and P(20) ≈ 0.90. There is a 20% chance that at least one tree is located within a circle having radius 2ft and a 90% chance for a circle having a radius 20 ft.
b) The larger the circle, the more likely it is to contain a tree. Y=1; probability cannot be greater than 1. They then show a graph with a window of [0, 25, 5] by [0, 1, 0]. But, I donít know what to put in for Y1 or any others if needed.
c) x≈6.1. A circle of radius 6.1 ft has a 50-50 chance of containing at least one tree.
Thanks so much.
--------------
P(2) = 0.20 and P(20) = 0.9 and the P(x=6.1)= 50% are all correct.
---
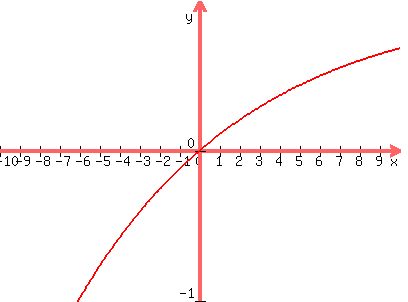
The graph is the graph of P(x) = 1-e^(-0.1144x)
If you let x = 2 you will read y = 0.20
If you let x = 20 you will read y = 0.90
If you let x = 6.1 you will read y = 0.50
====================
Cheers,
Stan H.
|
|
|