Question 271340: solve
(x+11)(x-18)(x+8)>0
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 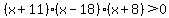
One way to solve this is- Graph the equation
 - Find the x values that make y positive. In other words find the x values where the graph is above the x-axis.
This method requires strong graphing skills. Another method depends on our understanding of multiplication and on some logic. This is the approach I will take.
This inequality says that a product of three factors is positive. Now how do we get a positive result when we multiply 3 factors? After a little thought we should know that there only two possibilities:- All three factors are positive.
- Two of the factors are negative and the third one is positive.
So how do we express these two possibilities algebraically? Well, the "all three factors are negative" possibility is fairly straightforward:
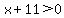 and and 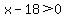 and and 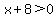
The "two positive and one negative" possibility is a little trickier:
(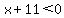 and and 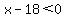 and and 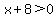 ) or ( ) or (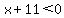 and and 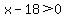 and and 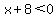 ) or ( ) or (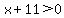 and and 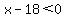 and and 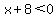 ) )
Expressing these together we get:
(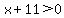 and and 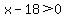 and and 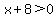 ) or (( ) or ((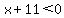 and and 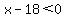 and and 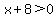 ) or ( ) or (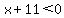 and and 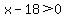 and and 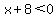 ) or ( ) or (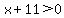 and and 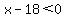 and and 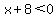 )) ))
We could go ahead and solve this. But if we're clever we can simplify these greatly before we solve them. With some thought we should be able to determine the order of the factors. Which is largest? Which is smallest? And which will also be in between? Regardless of what number x happens to be, won't x+11 always be larger than the other two? And won't x-18 always be the smallest? And x+8 will always be a number between x-18 and x+11. With this knowledge of the order and with some simple logic, we can simplify our expressions. For example, if the smallest of the three factors, x-18, is positive, won't the other two larger factors (which are to the right of on the number line) also be positive? So to find where all three factors are positive we only have to find where
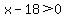
And for the "two negative and one positive" possibility, won't the positive factor have to be the largest factor, x+11? And if the middle factor is negative, won't the smallest one also have to be negative? So this possibility boils down to just:
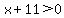 and and 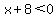
So the full solution can be found from:
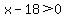 or ( or (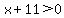 and and 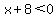 ) )
This is much easier than the earlier, much longer compound inequality. Solving these we get:
 or ( or (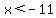 and and 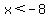 ) )
If you tried the graphing approach, here's what the graph should look like:

See how the graph is above the x-axis for x's that are greater than 18 and for x's that are between -11 and -8. (Note: The scale on the y-xis is different than that for the x-axis. I did this so you could more easily see the important parts of the graph.)
|
|
|