Question 270649: Given the equation x=4^-y, can you transform this expression into the equivalent logarithmic equation, and evaluate the equation for three values (0,0.5,1,2,3)?
Thank you
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! equation is x = 4^(-y)
take the log of both sides of this equation to get:
log(x) = log(4^(-y)
since log (x^a) = a*log(x), this equation becomes:
log(x) = -y*log(4)
divide both sides of this equation by -log(4) to get:
-log(x)/log(4) = y
this is the same as:
y = -log(x)/log(4)
solve this equation for the following values of x.
when x = 0, y = -log(0)/log(4) = undefined (can't take log of 0).
when x = .5, y = -log(.5)/log(4) = 0.5
when x = 1, y = -log(1)/log(4) = 0
when x = 2, y = -log(2)/log(4) = -0.5
when x = 3, y = -log(3)/log(4) = -0.79248125
A graph of this equation would look like this:
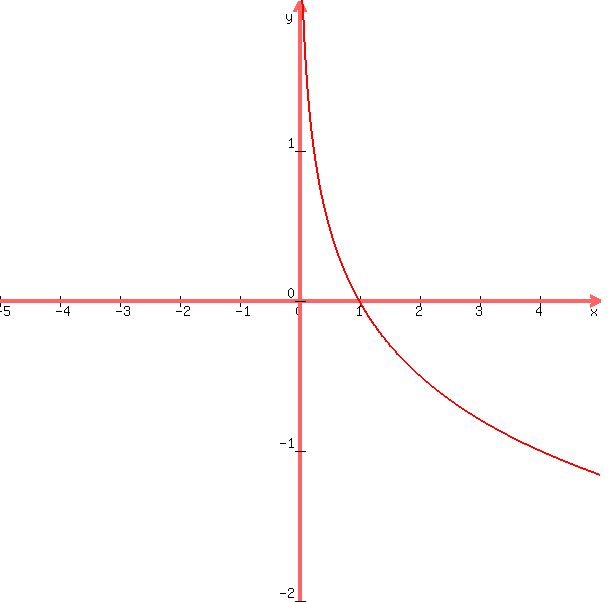
To solve this problem, you use the log function of your calculator.
For example, the equation:
when x = 3, y = -log(3)/log(4) = -0.79248125
becomes:
y = -.477121255 / .602059991 = -.79248125
Note that the log function of your calculator is the logarithm of a number to the base of 10.
To prove these answers are correct, we substitute them in the original equation.
The original equation is:
x = 4^(-y)
our answers were:
when x = 0, y = -log(0)/log(4) = undefined (can't take log of 0).
when x = .5, y = -log(.5)/log(4) = 0.5
when x = 1, y = -log(1)/log(4) = 0
when x = 2, y = -log(2)/log(4) = -0.5
when x = 3, y = -log(3)/log(4) = -0.79248125
substituting in the original equation, we get:
when y = undefined, we can't solve for x.
when y = .5, x = 4^(-y) becomes x = 4^(-.5) becomes x = .5 which is correct (see when x = .5).
when y = 0, x = 4^(-y) becomes x = 4^(0) becomes x = 1 which is correct (see when x = 1).
when y = -.5, x = 4^(-y) becomes x = 4^(.5) becomes x = 2 which is correct (see when x = 2).
when y = -0.79248125, x = 4^(-y) becomes x = 4^(.79248125) becomes x = 3 which is correct (see when x = 3).
The following is FYI.
You don't really need to know this to solve this problem, but it might help you understand logs a little better.
Logarithms and exponents are inverse relationships to each other, just like addition and subtraction are inverse relationships to each other, just like multiplication and division are inverse relationships to each other.
The basic addition identity states that:
y = x + 5 if and only if x = y - 5.
This means that subtraction is the inverse operation of addition.
The basic multiplication identity states that:
y = x*5 if and only if x = y/5.
This means that division is the inverse operation of multiplication.
Similarly, the basic logarithmic identity states that:
y = log(b,x) if and only if b^y = x
This means that y equals log of x to the base b if and only if the base b raised to the power of y equals x.
An example of this would be:
2 = log(10,100) if and only if 10^2 = 100.
We can apply this basic definition of logarithms to your original equation to get:
x = 4^(-y) if and only if -y = log(4,x).
if we multiply both sides of this equation by -1, we get:
y = -log(4,x)
we can solve this equation by converting the equation from the base of 4 to the base of 10.
the conversion formula states that that log(b,x) = log(c,x)/log(c,b).
This means that:
log of x to the base b is equivalent to log x to the base c divided by the log of the base b to the base c.
We can use this conversion formula to convert from the base of 4 to the base of 10.
We do this because the calculator can handle the base of 10 but it can't handle the base of 4.
our formula of:
y = -log(4,x) becomes:
y = -log(10,x)/log(10,4)
Since if you don't specify the base, log(x) assumes the base of 10 which means it assumes log(10,x), then this formula can be written as:
y = -log(x)/log(4)
If this looks very familiar to the formula we originally derived by taking the log of both sides of the original equation, that's no accident.
The equations are the same.
We simply arrived at the same equation from a different perspective.
|
|
|