Question 268286: Please help with this problem, this is what I have so far:
Problem: Height of a projected ball,
An astronaut on the moon throws a baseball upward. The astronaut is 6ft., 6in. tall, and the initial velocity of the ball is 30 ft. per sec. The height S of the ball in feet is given by the equation
S= -2.7t^2 + 30t + 6.5
where t is the number of seconds after the ball was thrown.
A.) After how many seconds is the ball 12ft above the moon's surface? Round to the nearest hundreth.
I know I have to look for the seconds, which is t so then I have to solve for S, the height. This is have I've got so far:
12 = 2.7t^2 + 30t + 6.5
-12 -12
------------------------
0 = 2.7t^2 + 30t - 5.5
B.)How many seconds will it take fore the ball to return to the surface? Round to the nearest hundredth.
So on the second part of the equation I have to look for the time, so that means that I have to solve for the height...
Thanks for your help in advance.
Found 2 solutions by Alan3354, scott8148:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! An astronaut on the moon throws a baseball upward. The astronaut is 6ft., 6in. tall, and the initial velocity of the ball is 30 ft. per sec. The height S of the ball in feet is given by the equation
S= -2.7t^2 + 30t + 6.5
where t is the number of seconds after the ball was thrown.
A.) After how many seconds is the ball 12ft above the moon's surface? Round to the nearest hundreth.
I know I have to look for the seconds, which is t so then I have to solve for S, the height. This is have I've got so far:
12 = 2.7t^2 + 30t + 6.5 *** It's -2.7
-12 -12
------------------------
0 = -2.7t^2 + 30t - 5.5
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=840.6 is greater than zero. That means that there are two solutions:  . .


Quadratic expression  can be factored: can be factored:

Again, the answer is: 0.18646247628908, 10.924648634822.
Here's your graph:
 |
---------------
Notice there are 2 numbers, the smallest is going up, the other coming back down.
-------------
B.)How many seconds will it take for the ball to return to the surface? Round to the nearest hundredth.
It's at the surface when h = 0
-2.7t^2 + 30t + 6.5 = 0
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=970.2 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 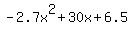 can be factored: can be factored:

Again, the answer is: -0.212598823296627, 11.3237099344077.
Here's your graph:
 |
------------
Ignore the negative number.
t = 11.32 seconds
So on the second part of the equation I have to look for the time, so that means that I have to solve for the height...
Answer by scott8148(6628)   (Show Source): (Show Source):
You can put this solution on YOUR website! A.) just use the quadratic formula on the equation you generated and solve for t
___ watch the signs (your equation has an incorrect sign for the coefficient of the squared term)
B.) substitute zero for S in the original equation (S= -2.7t^2 + 30t + 6.5) and use the quadratic formula
check the solutions for t to see if they make sense
___ A should have two solutions (upward and downward)
___ B should have one solution (negative value not realistic)
|
|
|