SOLUTION: The following problem is from my college algebra class using the book "Introduction to Algebra." A polynomial in x has a degree 3. The coefficient of x squared is 3 less than th

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: The following problem is from my college algebra class using the book "Introduction to Algebra." A polynomial in x has a degree 3. The coefficient of x squared is 3 less than th      Log On


   

Question 266446: The following problem is from my college algebra class using the book "Introduction to Algebra."
A polynomial in x has a degree 3. The coefficient of x squared is 3 less than the coefficient of x to the 3rd.? The coefficient of x is three times the coefficient of x squared. The remaining coefficient is 2 more than the coefficient of x to the third. The sum of the coefficients is -4. What is the polynomial?
I honestly don't even know where to begin, I started by using simple guesses and it got me nowhere. They assign us the most difficult question in the exercise set even though the text in no way prepares us for the answer. Please help!
Found 2 solutions by jim_thompson5910, stanbon:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
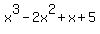"A polynomial in x has a degree 3" means that the polynomial has a x%5E3 term (and that term has the largest exponent). Examples of 3rd degree polynomials are x%5E3%2B6x-4, x%5E3-2x%5E2%2Bx%2B5, and x%5E3-1.



The most general 3rd degree polynomial is 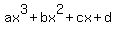ax%5E3%2Bbx%5E2%2Bcx%2Bd where a, b, c, d are all real numbers.


Since "The coefficient of x squared is 3 less than the coefficient of x to the 3rd", this means that b=a-3. Also, because "The coefficient of x is three times the coefficient of x squared", we know that c=3b. Furthermore, it's stated that "The remaining coefficient is 2 more than the coefficient of x to the third" which tells us that d=a%2B2. Finally, since "The sum of the coefficients is -4", we get a%2Bb%2Bc%2Bd=-4


So we basically have the four equations b=a-3, c=3b, d=a%2B2, and a%2Bb%2Bc%2Bd=-4


I'll let you solve this system. The basic idea is to form an equation with one variable, solve for that variable, and then use that solution to find the value of another variable. You'll continue this process until you find all 4 variables.

For example, plug b=a-3, c=3b, and d=a%2B2 into a%2Bb%2Bc%2Bd=-4 to get a%2B%28a-3%29%2B%283b%29%2B%28a%2B2%29=-4. After that, plug b=a-3 into a%2B%28a-3%29%2B%283b%29%2B%28a%2B2%29=-4 to get a%2B%28a-3%29%2B3%28a-3%29%2B%28a%2B2%29=-4. Now we have an equation with a single variable to solve for.

Answer by stanbon(75887) About Me  (Show Source):
You can put this solution on YOUR website!
A polynomial in x has a degree 3.
The coefficient of x squared is 3 less than the coefficient of x to the 3rd. The coefficient of x is three times the coefficient of x squared.
The remaining coefficient is 2 more than the coefficient of x to the third. The sum of the coefficients is -4. What is the polynomial?
-------------
y = kx^3 + (k-3)x^2 + (3k-9)x +(k+2)
----------------------------------------
Equation:
k + (k-3) + 3k-9 + k+2 = -4
6k -10 = -4
6k = 6
k = 1
----
Polynomial:
y = x^3 - 2x^2 -6x + 3
=============================
Cheers,
Stan H.