SOLUTION: How to find a “third” first-degree factor of 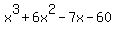x^3 + 6x^2 – 7x – 60

Since the coefficient of the highest power of x is 1, then if there
ia a first degree factor, it will be of the form 

x ± r

where r is a factor of the absolute value of the constant term, which
in this case is -60.

So we list the factors of |-60|, or 60.  They are

1,2,3,4,5,6,10,12,15,20,30,60

try 1, using synthetic division:

1 | 1  6  -7  -60
  |    1   7    0
    1  7   0  -60

Nope, that leaves -60 remainder.

try 2, using synthetic division:

2 | 1  6  -7  -60
  |    2  16   18
    1  8   9  -42

Nope, that leaves -42 remainder.

try 3, using synthetic division:

3 | 1  6  -7  -60
  |    3  27   60
    1  9  20    0

Yep! That leaves a 0 remainder.

Therefore we have factored  

 

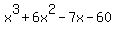as



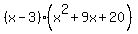We got the coefficients in the second parentheses
from the numbers 1 9 20 at the bottom of the 
synthetic division above.

Now we can factor the second parenthese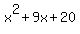s 
as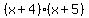 

And the final factored form is



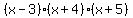Edwin