Question 26451: ok so i thought i understood this radical stuff so i need you to explain things in lamen terms for me, # do not work with my head well.
first of all i know the definitions of factors and terms but when it comes down to the problem i just cancel ne thing cause i don't know which is which
so heres one of my questions
heres how i did it:
4x-12/x^2 * 7x+21/28
so i factored the numerators first and got
2*2(x-3) * 7(x+3)
then i factored the demonminators and got
(x-3)(x-3) * 2*2*7
so i canceled out 2*2 on the top and the 2*2 on the bottom, then the (x-3)'s on the top and bottom of the first equation. then the (x+3)'s on the top and bottom of the second equation and then both 7's on the second equation top and bottom
and the answer i got was 0
i didn't know if that was possible to get, maybe i did it right. but its these types of questions that just mess me up. i will prolly be writing for some more help on LCD and stuff like that.
thanx for you help in advance
shanna
Answer by longjonsilver(2297)   (Show Source):
You can put this solution on YOUR website! Shanna,
The problem that most students who struggle with a topic like algebra is that they do not understand the basic rules and when to apply them. And importantly when you cannot apply certain rules.
What they end up doing is so much more complicated than the correct method.
Here goes:
Now, this is a fraction, primarily, just like 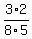 . The beauty of maths is that the rules applied to easier questions are exactly the same as those applied to "harder" questions...
OK... we can factorise if we WISH to, to give 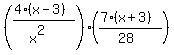 , but the question is one of fractions multiplied, so we basically just need to do that multiplication. Before that, I notice that the second fraction has a 7 on the top and a 28 on the bottom...these can be reduced...
Lets combine both fractions then...
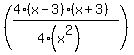
Now, we have a single expression where terms are all held together by multiplication and division, just like (4*3*5)/(4*7) is, as an example. In this simpler expression, we can simplify to give (3*5)/(7) since we had "multiply by 4" on the top and then "divide by 4"..opposite processes that cancel each other.
So, our question becomes 
And this is an answer, in factorised form. There is nothing else we can cancel.
As you can see, i actually did far less work than you did :-)
jon.
|
|
|
