SOLUTION: For a certain three digit positive number the ones digit is 3 times the hundreds digit. The tens digit is 1 less than the ones digit. The ones digit is 15 less than the product of

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: For a certain three digit positive number the ones digit is 3 times the hundreds digit. The tens digit is 1 less than the ones digit. The ones digit is 15 less than the product of       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 263976: For a certain three digit positive number the ones digit is 3 times the hundreds digit. The tens digit is 1 less than the ones digit. The ones digit is 15 less than the product of the hundreds and tens digit. What digit is the ones digit?
Answer by JBarnum(2146) About Me  (Show Source):
You can put this solution on YOUR website!
For a certain three digit positive number the ones digit is 3 times the hundreds digit. The tens digit is 1 less than the ones digit. The ones digit is 15 less than the product of the hundreds and tens digit. What digit is the ones digit?
first take each line by line
"For a certain three digit positive number" means: xyz
using xyz as the 3 digit number: ones digit= z, tens digit= y, hundreds digit=x
"ones digit is 3 times the hundreds digit"means: z=3x
"The tens digit is 1 less than the ones digit" means: y=z-1
"The ones digit is 15 less than the product of the hundreds and tens digit" means: z=xy-15
"What digit is the ones digit?" means z=?
since we are looking for z rearange the first equation z=3x to x=z/3 so relist your equations:
x=z/3 y=z-1 z=xy-15
we want to find value for z and they give value for y and you just got the value for x, so in the third equation put the z/3 for x and the z-1 for y:
z=xy-15
z=((z/3)(z-1))-15 now simplify
z= ((z^2-z)/3)-15 id get rid of the fraction by multiplying everything by 3
3z= z^2-z-45 subtract 3z from both sides
0= z^2-z-45-3z simplify
0= z^2-4z-45 Standard Quadratic equation A=1 B=-4 C=-45
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation az%5E2%2Bbz%2Bc=0 (in our case 1z%5E2%2B-4z%2B-45+=+0) has the following solutons:

z%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-4%29%5E2-4%2A1%2A-45=196.

Discriminant d=196 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--4%2B-sqrt%28+196+%29%29%2F2%5Ca.

z%5B1%5D+=+%28-%28-4%29%2Bsqrt%28+196+%29%29%2F2%5C1+=+9
z%5B2%5D+=+%28-%28-4%29-sqrt%28+196+%29%29%2F2%5C1+=+-5

Quadratic expression 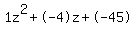1z%5E2%2B-4z%2B-45 can be factored:
1z%5E2%2B-4z%2B-45+=+1%28z-9%29%2A%28z--5%29
Again, the answer is: 9, -5. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-4%2Ax%2B-45+%29


To reiterate the question that you gave us to solve
"What digit is the ones digit?"
I did answer it, check the quadratic equation again (x=9,-5), and since it cant be negative the ones digit must be 9.
**oh and if you want to know what the other 2 digits are reread the question knowing the ones digit is 9 so we know xy9
9/3=x x=3 now we know 3y9
y=9-1=8 now we know 389. but this number isnt the answer to the question you stated above