Question 263527:  , x<= 0 , x<= 0
we're supposed to find the inverse of the power function, my teacher is lazy and dosnt teach us much. the answer i got was 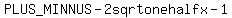 he marked it wrong... he marked it wrong...
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website! we're supposed to find the inverse of the power function, my teacher is lazy and dosnt teach us much. the answer i got was 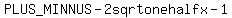 he marked it wrong... he marked it wrong...
First of all, the answer you gave is not a function, with the
"positive or negative". No function can have a "±" in it.
Let's draw the graph of f(x) first.
Now if the domain  weren't given and we just plotted weren't given and we just plotted
 we'd have this graph:
we'd have this graph:
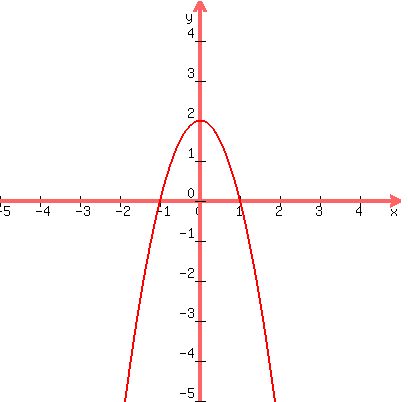 That graph passes the vertical line test, because no vertical
line crosses the graph more than once, so it is a function.
However it is not a one-to-one function because it does not
pass the horizontal line test. If you draw a horizontal line
through it it will cut the graph twice. So it does not have
an inverse function.
However since
That graph passes the vertical line test, because no vertical
line crosses the graph more than once, so it is a function.
However it is not a one-to-one function because it does not
pass the horizontal line test. If you draw a horizontal line
through it it will cut the graph twice. So it does not have
an inverse function.
However since  is given for its domain, the graph
of f(x) is NOT the one above. Here is the graph of is given for its domain, the graph
of f(x) is NOT the one above. Here is the graph of
 with the given domain with the given domain 
 It consists only of the left half of the graph of
It consists only of the left half of the graph of  without the given domain
without the given domain  So you see now that the function passes not only the VERTICAL line
test, it passes the HORIZONTAL line test as well. So with that
restricted domain, it DOES have an inverse.
Now let's sketch the inverse before finding its equation. First draw
the line whose equation is
So you see now that the function passes not only the VERTICAL line
test, it passes the HORIZONTAL line test as well. So with that
restricted domain, it DOES have an inverse.
Now let's sketch the inverse before finding its equation. First draw
the line whose equation is  , called the IDENTITY line
(because x and y are indentically equal if you have y=x). Let's
draw that line. It is a line through the origin which goes at a
45° angle to both axes. I'll draw it dotted and in green , called the IDENTITY line
(because x and y are indentically equal if you have y=x). Let's
draw that line. It is a line through the origin which goes at a
45° angle to both axes. I'll draw it dotted and in green
 Now the inverse of f(x) is the reflection of the graph of
f(x) into that green dotted identity line, whose equation is y=x.
I'll draw it in blue:
Now the inverse of f(x) is the reflection of the graph of
f(x) into that green dotted identity line, whose equation is y=x.
I'll draw it in blue:
 The inverse of a function is a function symmetric with the
original function's graph about the identity line, y=x.
Now let's find the equation of that inverse.
The inverse of a function is a function symmetric with the
original function's graph about the identity line, y=x.
Now let's find the equation of that inverse.
 , x<= 0
1. Change f(x) to y , x<= 0
1. Change f(x) to y
 2. Interchange x and y
2. Interchange x and y
 3. Solve for y:
3. Solve for y:


 Now looking at the graph, the blue inverse graph
is entirely below the x-axis. Therefore
we can only take the negative square root,
and ignore the positive square root.
Now looking at the graph, the blue inverse graph
is entirely below the x-axis. Therefore
we can only take the negative square root,
and ignore the positive square root.
 4. Finally change y to
4. Finally change y to   So the final answer is
So the final answer is
   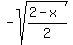 Your teacher might expect you to rationalize the denominator.
If so the final answer is
Your teacher might expect you to rationalize the denominator.
If so the final answer is
   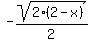 or
or
   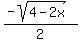 Edwin
Edwin
|
|
|